Question

17．如图1，CA=CB，CD=CE，∠ACB=∠DCE=a，AD、BE交于点H，连CH．
（1）求∠AHE的度数；（用a表示）
（2）如图2，连接CH，求证：CH平分∠AHE；
（3）如图3，若a=60°，P，Q 分别是AD，BE的中点，连接CP，PQ，CQ．请判断三角形PQC的形状，并证明．

Answer 1

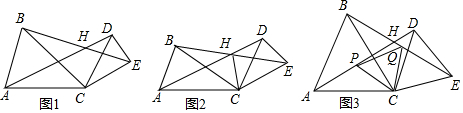
分析 （1）由条件可证明△ACD≌△BCE，可得∠CAD=∠CBE，再利用三角形内角及外角的性质可求得∠AHE；
（2）过点C作CM⊥AD于M，CN⊥BE于N，可证明△ACM≌△BCN，可证得CM=CN，利用角平分线的判定可证明结论；
（3）由条件先证明△APC≌△BQC，可求得∠PCA=∠QCB，则可证明△PCQ为正三角形．

解答 （1）解：
∵∠ACB=∠DCE=α，
∴∠ACD=∠BCE，
在△ACD和△BCE中
$\left\{\begin{array}{l}{CA=CB}\\{∠ACD=∠BCE}\\{CD=CE}\end{array}\right.$
∴△ACD≌△BCE（SAS），
∴∠CAD=∠CBE，
∵∠AMC=∠AMC，
∴∠AHB=∠ACB=α，
∴∠AHE=180°-α，；
（2）证明：过点C作CM⊥AD于M，CN⊥BE于N，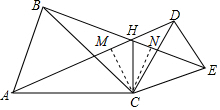

∵△ACD≌△BCE，
∴∠CAM=∠CBN，
在△ACM和△BCN中
$\left\{\begin{array}{l}{∠CAM=∠CBN}\\{∠AMC=∠BNC=90°}\\{AC=BC}\end{array}\right.$
∴△ACM≌△BCN（AAS），
∴CM=CN，
∴CH平分∠AHE；
（3）解：△CPQ是等边三角形，
理由如下：
∵△ACD≌△BCE，
∴AD=BE，∠PAC=∠QBC，
∵P、Q分别是AD、BE的中点，
∴AP=BQ，
在△APC和△BQC中
$\left\{\begin{array}{l}{AP=BQ}\\{∠PAC=∠QBC}\\{AC=BC}\end{array}\right.$
∴△APC≌△BQC（SAS），
∴CP=CQ，∠PCA=∠QCB，
∴∠PCQ=∠ACB=60°，
∴△CPQ是正三角形．

点评 本题主要考查全等三角形的判定和性质，掌握全等三角形的判定方法（即SSS、SAS、ASA、AAS和HL）和性质（全等三角形的对应边相等、对应角相等）．