题目内容
在△ABC中,∠C=90°,cosA=
,AC=6,则AB的长度为( )
| 3 |
| 5 |
| A、8 | B、10 | C、12 | D、14 |
考点:解直角三角形
专题:计算题
分析:根据余弦的定义得到cosA=
=
,然后利用比例性质求AB.
| AC |
| AB |
| 3 |
| 5 |
解答:解:在△ABC中,∠C=90°,、
∵cosA=
=
,
∴AB=
×6=10.
故选B.
∵cosA=
| AC |
| AB |
| 3 |
| 5 |
∴AB=
| 5 |
| 3 |
故选B.
点评:本题考查了解直角三角形:在直角三角形中,由已知元素求未知元素的过程就是解直角三角形.

练习册系列答案
 天天练口算系列答案
天天练口算系列答案
相关题目
 已知二次函数的图象(-3≤x≤0)如图所示.关于该函数在所给自变量取值范围内,下列说法正确的是( )
已知二次函数的图象(-3≤x≤0)如图所示.关于该函数在所给自变量取值范围内,下列说法正确的是( )| A、有最大值1,无最小值 |
| B、有最大值1,有最小值0 |
| C、有最大值1,有最小值-3 |
| D、有最大值0,有最小值-3 |
在Rt△ABC中,∠C=90°,a、b、c分别是∠A、∠B、∠C的对边,下列等式中正确的是( )
A、cosA=
| ||
B、sinB=
| ||
C、tanB=
| ||
D、cotA=
|
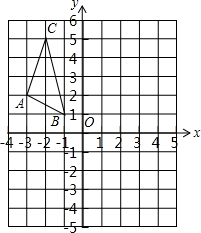 如图,在平面直角坐标系xOy中,点A,B,C的坐标分别为(-3,2),(-1,1),(-2,5).
如图,在平面直角坐标系xOy中,点A,B,C的坐标分别为(-3,2),(-1,1),(-2,5). 如图,OA=10,OB=6,∠xOA=60°,∠xOB=135°,求A,B两点坐标.
如图,OA=10,OB=6,∠xOA=60°,∠xOB=135°,求A,B两点坐标. 如图,有一个可以自由转动的转盘被平均分成4个扇形,分别标有1、2、3、4四个数字,小王和小李各转动一次转盘为一次游戏.当每次转盘停止后,指针所指扇形内的数为各自所得的数,一次游戏结束得到一组数(若指针指在分界线时重转).
如图,有一个可以自由转动的转盘被平均分成4个扇形,分别标有1、2、3、4四个数字,小王和小李各转动一次转盘为一次游戏.当每次转盘停止后,指针所指扇形内的数为各自所得的数,一次游戏结束得到一组数(若指针指在分界线时重转).