题目内容
15.(1)如图1,已知EF∥BC,∠1=∠B.问:DF与AB平行吗?请说明理由.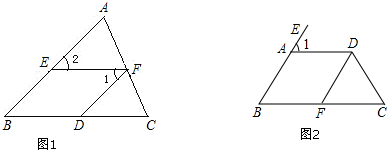
(2)如图2,AD∥BC,∠B=60°,∠1=∠C.
①求∠C的度数.
②如果DF为∠ADC的平分线,那么DF与AB平行吗?说明理由.
分析 (1)根据平行线的性质得出∠1=∠FDC,求出∠B=∠FDC,根据平行线的判定得出即可;
(2)①根据平行线的性质得出∠1=∠B=60°,根据∠1=∠C求出即可;
②根据平行线的性质得出∠C+∠CDA=180°,求出∠CDA=120°,根据角平分线定义求出∠ADF=$\frac{1}{2}∠$CDA=60°,根据平行线的性质得出∠DFC=∠ADF=60°,求出∠B=∠DFC,根据平行线的判定得出即可.
解答 (1)解:DF∥AB,
理由是:∵EF∥BC,
∴∠1=∠FDC,
∵∠1=∠B,
∴∠B=∠FDC,
∴DF∥AB;
(2)解:①∵AD∥BC,∠B=60°,
∴∠1=∠B=60°,
∵∠1=∠C,
∴∠C=60°;
②DF∥AB,
理由是:∵AD∥BC,
∴∠C+∠CDA=180°,
∵∠C=60°,
∴∠CDA=120°,
∵DF平分∠CDA,
∴∠ADF=$\frac{1}{2}∠$CDA=60°,
∵AD∥BC,
∴∠DFC=∠ADF=60°,
∵∠B=60°,
∴∠B=∠DFC,
∴DF∥AB.
点评 本题考查了平行线的判定和性质的应用,能正确运用定理进行推理是解此题的关键,注意:平行线的判定有:①同位角相等,两直线平行,②内错角相等,两直线平行,③同旁内角互补,两直线平行,反之亦然.

练习册系列答案
相关题目
4.试估计$\sqrt{5}$的大小( )
| A. | 在2与3之间 | B. | 在3与4之间 | C. | 在4与5之间 | D. | 在5与6之间 |
5.下列方程组中,是二元一次方程组的为( )
| A. | $\left\{\begin{array}{l}{x+y=1}\\{x-z=2}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{{y}^{2}-1=0}\\{x-2y=0}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{y-2x=1}\\{y=5}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{\frac{1}{x}+3y=0}\\{x-y=1}\end{array}\right.$ |
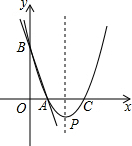 如图,直线y=-3x+3与x轴、y轴分别交于点A、B,抛物线y=a(x-2)2+k经过点A,B,并与x轴交于另一点C,其顶点为P.
如图,直线y=-3x+3与x轴、y轴分别交于点A、B,抛物线y=a(x-2)2+k经过点A,B,并与x轴交于另一点C,其顶点为P.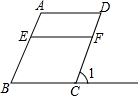 如图,E在AB上,F在DC上,G是BC延长线上的一点:
如图,E在AB上,F在DC上,G是BC延长线上的一点: 如图,四边形ABCD向右平移一段距离后得到四边形A′B′C′D′.
如图,四边形ABCD向右平移一段距离后得到四边形A′B′C′D′.