题目内容
13.小惠在纸上画了一条数轴后,折叠纸面,使数轴上表示l的点与表示-3的点重合,若数轴上A、B两点之间的距离为8(A在B的左侧),且A、B两点经上述折叠后重合,则A点表示的数为-5.分析 若1表示的点与-3表示的点重合,则折痕经过-1;若数轴上A、B两点之间的距离为8,则两个点与-1的距离都是4,再根据点A在B的左侧,即可得出答案.
解答 解:画出数轴如下所示:
依题意得:两数是关于1和-3的中点对称,即关于(1-3)÷2=-1对称;
∵A、B两点之间的距离为8且折叠后重合,则A、B关于-1对称,又A在B的左侧,
∴A点坐标为:-1-8÷2=-1-4=-5.
故答案为:-5.
点评 本题考查了数轴的知识,注意根据轴对称的性质,可以求得使两个点重合的折痕经过的点所表示的数即是两个数的平均数.

练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
1.下列说法正确的是( )
| A. | 为了解全国中学生的心理健康情况,应该采用普查的方式 | |
| B. | 一个游戏的中奖概率是0.1,则做10次这样的游戏一定会中奖 | |
| C. | 为了调查中秋节期间市场上月饼质量情况,应该采用抽样调查的方式 | |
| D. | 若甲组数据的方差S甲2=0.01,乙组数据的方差S乙2=0.1,则乙组数据比甲级稳定 |
18.一位病人发高烧进医院治疗,医生给他开了药、挂了水,同时护士每隔1小时为病人测体温,及时了解病人的好转情况.下表记载的是护士对病人测体温的变化数据:
注:病人早晨进院时医生测得病人体温是40.2℃.
问:(1)把上升的体温记为正数,下降的体温记为负数,请填写上表;
(2)病人什么时候体温达到最高,最高体温是多少?
(3)病人中午12点时体温多高?
(4)病人几点后体温稳定正常(正常体温是37℃).
| 时间 | 7:00 | 8:00 | 9:00 | 10:00 | 11:00 | 12:00 | 13:00 | 14:00 | 15:00 |
| 体温(与前一次比较) | 升0.2 | 降1.0 | 降0.8 | 降1.0 | 降0.6 | 升0.4 | 降0.2 | 降0.2 | 降0 |
| +0.2 | 0 |
问:(1)把上升的体温记为正数,下降的体温记为负数,请填写上表;
(2)病人什么时候体温达到最高,最高体温是多少?
(3)病人中午12点时体温多高?
(4)病人几点后体温稳定正常(正常体温是37℃).
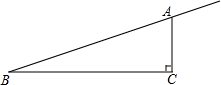 如图,在Rt△ABC中,∠ACB=90°,AC=1cm,BC=4cm,动点P从点B出发,以每秒1cm的速度沿射线BA运动,求出点P运动所有的时间,使得△PBC为等腰三角形.
如图,在Rt△ABC中,∠ACB=90°,AC=1cm,BC=4cm,动点P从点B出发,以每秒1cm的速度沿射线BA运动,求出点P运动所有的时间,使得△PBC为等腰三角形.