题目内容
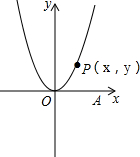 如图,P是抛物线y=x2上第一象限内的点,A点坐标为(6,0).
如图,P是抛物线y=x2上第一象限内的点,A点坐标为(6,0).(1)若P点的坐标为(x,y),△POA的面积为S,求出S与x的关系;
(2)当S=6时,求P点的坐标;
(3)在抛物线y=x2上求出一点P′,使P′0=P′A,求出P′的坐标.
考点:二次函数的性质,二次函数图象上点的坐标特征
专题:
分析:(1)已知A点坐标为(6,0),可以得到OA=6,△POA中OA边上的高就是P点的纵坐标.根据三角形的面积公式就可以求出.
(2)把S=6代入(1)中求得的函数解析式,求出x的值,就可以得到P点的坐标.
(3)使P′O=P′A,则P′一定在线段OA的垂直平分线上,OA的垂直平分线的解析式是x=3,因而把x=3代入函数y=x2的解析式,就可以求出点的纵坐标.
(2)把S=6代入(1)中求得的函数解析式,求出x的值,就可以得到P点的坐标.
(3)使P′O=P′A,则P′一定在线段OA的垂直平分线上,OA的垂直平分线的解析式是x=3,因而把x=3代入函数y=x2的解析式,就可以求出点的纵坐标.
解答: 解:(1)过P作PH⊥x轴于H,则S=
解:(1)过P作PH⊥x轴于H,则S=
OA•PH=
×6•y=3y=3x2,
(2)当S=6时,3x2=6,
∴x=±
,且P在第一象限,
∴P(
,
).
(3)∵P′O=P′A,则P′在线段OA的中垂线上,
∴P′的横坐标为3,
又∵当x=3时,y=9,
∴P′(3,9).
 解:(1)过P作PH⊥x轴于H,则S=
解:(1)过P作PH⊥x轴于H,则S=| 1 |
| 2 |
| 1 |
| 2 |
(2)当S=6时,3x2=6,
∴x=±
| ||
| 2 |
∴P(
| ||
| 2 |
| 1 |
| 2 |
(3)∵P′O=P′A,则P′在线段OA的中垂线上,
∴P′的横坐标为3,
又∵当x=3时,y=9,
∴P′(3,9).
点评:考查了二次函数,本题是二次函数的解析式的求解,与线段的垂直平分线的判定方法,相结合的问题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 在如图所示的两个相似四边形中,∠C=125°,∠A=80°,∠B=75°,求x,y,∠D1.
在如图所示的两个相似四边形中,∠C=125°,∠A=80°,∠B=75°,求x,y,∠D1. 今年某区为绿化车道,用25600元购买甲、乙两种树苗共500棵,且这批树苗的成活率恰好为92%.有关甲、乙两种树苗的信息如图所示.
今年某区为绿化车道,用25600元购买甲、乙两种树苗共500棵,且这批树苗的成活率恰好为92%.有关甲、乙两种树苗的信息如图所示.