题目内容
16．
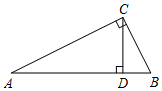如图，在Rt△ABC中，∠ACB=90°，CD⊥AB于D，如果AC=2$\sqrt{5}$，且tan∠ACD=2．求AB的长．
分析 首先根据AC=2$\sqrt{5}$，tan∠ACD=2求得BC的长，然后利用勾股定理求得AB的长即可．
解答 解：在Rt△ABC中，
∵∠ACB=90°，CD⊥AB，
∴∠B=∠ACD，
∵tan∠ACD=2，
∴tan∠B=$\frac{AC}{BC}=2$，
∴$BC=\sqrt{5}$，
由勾股定理得AB=5．
点评 本题考查了解直角三角形的知识，解题的关键是能够从题目中整理出直角三角形并选择合适的边角关系求解，难度不大．
练习册系列答案
活力课时同步练习册系列答案
相关题目
如图，△ABC内接于⊙O，直径DE⊥AB于点F，交BC于点 M，DE的延长线与AC的延长线交于点N，连接AM． 
1．小樱要到距家1200米的学校上学，一天，小樱出发10分钟后，小樱的爸爸立即去追赶小樱，且在距离学校200米的地方相遇．已知爸爸比小樱的速度快100米/分，求小樱的速度．若设小樱速度是x米/分，则根据题意所列方程正确的是（ ）
| A． | $\frac{1000}{x-100}$-$\frac{1000}{x}$=10 | B． | $\frac{1000}{x}$=$\frac{1000}{x+100}$+10 | ||
| C． | $\frac{1000}{x}$=$\frac{1000}{x-100}$+10 | D． | $\frac{1000}{x+100}$-$\frac{1000}{x}$=10 |