题目内容
 如图,⊙O是等边△ABC的外接圆,⊙O的半径为4,则等边△ABC的边长为________.
如图,⊙O是等边△ABC的外接圆,⊙O的半径为4,则等边△ABC的边长为________.
4
分析:首先连接OB,OC,过点O作OD⊥BC于D,由⊙O是等边△ABC的外接圆,即可求得∠OBC的度数,然后由三角函数的性质即可求得OD的长,又由垂径定理即可求得等边△ABC的边长.
解答: 解:连接OB,OC,过点O作OD⊥BC于D,
解:连接OB,OC,过点O作OD⊥BC于D,
∴BC=2BD,
∵⊙O是等边△ABC的外接圆,
∴∠BOC= ×360°=120°,
×360°=120°,
∵OB=OC,
∴∠OBC=∠OCB= =
= =30°,
=30°,
∵⊙O的半径为4,
∴OA=4,
∴BD=OB•cos∠OBD=4×cos30°=4× =2
=2 ,
,
∴BC=4 .
.
∴等边△ABC的边长为4 .
.
故答案为:4 .
.
点评:此题考查了垂径定理,圆的内接等边三角形,以及三角函数的性质等知识.此题难度不大,解题的关键是掌握数形结合思想的应用与辅助线的作法.

分析:首先连接OB,OC,过点O作OD⊥BC于D,由⊙O是等边△ABC的外接圆,即可求得∠OBC的度数,然后由三角函数的性质即可求得OD的长,又由垂径定理即可求得等边△ABC的边长.
解答:
 解:连接OB,OC,过点O作OD⊥BC于D,
解:连接OB,OC,过点O作OD⊥BC于D,∴BC=2BD,
∵⊙O是等边△ABC的外接圆,
∴∠BOC=
 ×360°=120°,
×360°=120°,∵OB=OC,
∴∠OBC=∠OCB=
 =
= =30°,
=30°,∵⊙O的半径为4,
∴OA=4,
∴BD=OB•cos∠OBD=4×cos30°=4×
 =2
=2 ,
,∴BC=4
 .
.∴等边△ABC的边长为4
 .
.故答案为:4
 .
.点评:此题考查了垂径定理,圆的内接等边三角形,以及三角函数的性质等知识.此题难度不大,解题的关键是掌握数形结合思想的应用与辅助线的作法.

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目
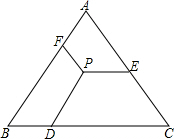 如图,△ABC是等边三角形,点P是三角形内的任意一点,PD∥AB,PE∥BC,PF∥AC,若△ABC的周长为12,则PD+PE+PF=( )
如图,△ABC是等边三角形,点P是三角形内的任意一点,PD∥AB,PE∥BC,PF∥AC,若△ABC的周长为12,则PD+PE+PF=( ) 31、如图,△ABC是等边三角形,AD是△ABC的角平分线,延长AC到E,使得CE=CD.
31、如图,△ABC是等边三角形,AD是△ABC的角平分线,延长AC到E,使得CE=CD.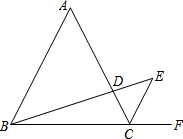 (2013•崇明县一模)如图,△ABC是等边三角形,且AD•ED=BD•CD.
(2013•崇明县一模)如图,△ABC是等边三角形,且AD•ED=BD•CD.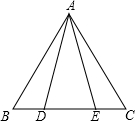 如图,△ABC是等边三角形,AD=AE,BE=CD.图中全等三角形有
如图,△ABC是等边三角形,AD=AE,BE=CD.图中全等三角形有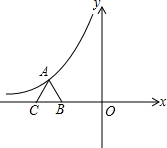 如图,△ABC是等边三角形,点A在反比例函数y=-
如图,△ABC是等边三角形,点A在反比例函数y=-