Question

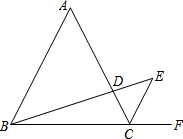（2013•崇明县一模）如图，△ABC是等边三角形，且AD•ED=BD•CD．
（1）求证：△ABD∽△CED；
（2）若AB=6，AD=2CD，求BE的长．

Answer 1

分析：（1）由AD•ED=BD•CD可知

AD

CD

=

BD

DE

，再根据∠ADB=∠CDE即可得出结论；
（2）过点D作DF⊥AB于点F，由（1）知△ABD∽△CED，再根据AB=6，AD=2CD可得出DE：BD=1：2，再根据△ABC是等边三角形可求出AD的长∠A的度数，根据直角三角形的性质求出DF及AF的长，进而可得出BF的长，在Rt△ADF中，根据勾股定理可求出BD的长，设DE=x，则BD=2x，可求出x的长，进而得出结论．

解答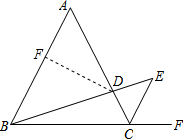：（1）证明：∵AD•ED=BD•CD，
∴

AD

CD

=

BD

DE

，
∵∠ADB=∠CDE，
∴△ABD∽△CED；

（2）解：过点D作DF⊥AB于点F，
∵△ABC是等边三角形，△ABD∽△CED，AB=6，AD=2CD，
∴

CD

AD

=

DE

BD

=

1

2

，
∴AD=

2

3

×6=4，CD=2，∠A=60°，
∴DF=AD•sinA=4×

3

2

=2

3

，AF=AD•cosA=4×

1

2

=2，
∴BF=AB-AF=6-2=4，
在Rt△ADF中，
∵BF=4，DF=2

3

，
∴BD=

BF2+DF2

=

42+(2 3 )2

=2

7

，
∵

CD

AD

=

DE

BD

=

1

2

，
∴设DE=x，则BD=2x，
∴2x=2

7

，解得x=

7

，
∴BE=BD+DE=2x+x=3x=3

7

．

点评：本题考查的是相似三角形的判定与性质，涉及到等边三角形的性质、直角三角形的性质等相关知识，难度适中．