题目内容
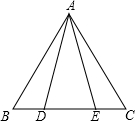如图，△ABC是等边三角形，AD=AE，BE=CD．图中全等三角形有2
2
对．分析：图中全等三角形有两对，△ABD≌△ACE，△ABE≌△ACD，先根据三角形ABC为等边三角形，由等边三角形的性质得到其三个内角都相等，三条边都相等，然后再根据已知AD=AE，BE=CD，由“SSS”得到△ABE≌△ACD；在BE=CD等式两边都减去DE，得到BD=CE，然后利用“SAS”得到△ABD≌△ACE．
解答：解：图中全等三角形有2对，分别为△ABD≌△ACE，△ABE≌△ACD，
证明：∵△ABC为等边三角形，
∴∠B=∠C=60°，AB=AC，
在△ABE和△ACD中，
AB=AC，BE=CD，AE=AD，
∴△ABE≌△ACD；
由BE=CD得，BE-DE=CD-DE，即BD=CE，
在△ABD和△ACE中，
AB=AC，∠B=∠C，BD=CE，
∴△ABD≌△ACE．
故答案为：2
证明：∵△ABC为等边三角形，
∴∠B=∠C=60°，AB=AC，
在△ABE和△ACD中，
AB=AC，BE=CD，AE=AD，
∴△ABE≌△ACD；
由BE=CD得，BE-DE=CD-DE，即BD=CE，
在△ABD和△ACE中，
AB=AC，∠B=∠C，BD=CE，
∴△ABD≌△ACE．
故答案为：2
点评：此题属于结论开放题，在给定条件下，探求全等三角形结论，一种方法可根据对称性划分，另一种方法可根据等腰三角形性质和全等三角形的条件去寻求．开放型试题重在开发思维，提高数学素养，是近几年中考的热点题型．
练习册系列答案
名题训练系列答案
期末集结号系列答案
相关题目
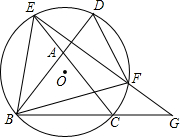∥AC，EF的延长线交BC的延长线于点G．
9、如图，△ABC是等边三角形，过AB边上一点D作BC的平行线交AC于E，则△ADE的三个内角
如图，△ABC是等边三角形，AB=4cm，则BC边上的高AD等于
如图，△ABC是等边三角形，D为BC边上的点，∠BAD=15°，将△ABD绕点A点逆时针方向旋转后到达△ACE的位置，那么旋转角的度数是
如图，△ABC是等边三角形，CE是外角平分线，点D在AC上，连结BD并延长与CE交于点E．