题目内容
已知:抛物线y=x2+bx+c经过点(2,-3)和(4,5).
(1)求抛物线的表达式及顶点坐标;
 (2)将抛物线沿x轴翻折,得到图象G,
(2)将抛物线沿x轴翻折,得到图象G,
求图象G的表达式;
(3)在(2)的条件下,当-2<x<2时,
直线y=m与该图象有一个公共点,
求m的值或取值范围.
解:(1)把(2,-3)和(4,5)分别代入y=x²+bx+c
得: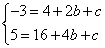 ,解得:
,解得: ,
,
∴抛物线的表达式为:y=x²-2x-3. ………………1分.
 ∵y=x²-2x-3=(x-1)2-4.
∵y=x²-2x-3=(x-1)2-4.
∴顶点坐标为(1,-4). ………………………2分.
(2)∵将抛物线沿x轴翻折,
得到图象G与原抛物线图形关于x轴对称,
∴图像G的表达式为:y=-x²+2x+3. ………3分.
(3)如图,当0≤x<2时,y=m过抛物线顶点(1,4)时,
直线y=m与该图象有一个公共点,
此时y=4,∴m=4. ………………4分
当-2<x<0时,直线y=m与该图象有一个公共点,
当y=m过抛物线上的点(0,3)时, y=3,∴m=3.
当y=m过抛物线上的点(-2,-5)时, y=-5,∴m=-5.
∴-5<m<3.
综上:m的值为4,或-5<m≤3. …………………………………5分.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案
相关题目
 有两个不相等的实数根,求
有两个不相等的实数根,求 的取值范围.
的取值范围. 中,∠C=90°,AC=4, BC=3,则以2.5为半径的⊙C与直线AB的位置关系
中,∠C=90°,AC=4, BC=3,则以2.5为半径的⊙C与直线AB的位置关系
 ,则tanA等于( )
,则tanA等于( ) C.
C. D.
D.