题目内容
6.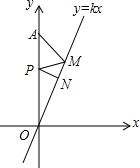 如图,已知正比例函数y=kx(k>0)的图象与x轴相交所成的锐角为70°,定点A的坐标为(0,4),P为y轴上的一个动点,M、N为函数y=kx(k>0)的图象上的两个动点,则AM+MP+PN的最小值为( )
如图,已知正比例函数y=kx(k>0)的图象与x轴相交所成的锐角为70°,定点A的坐标为(0,4),P为y轴上的一个动点,M、N为函数y=kx(k>0)的图象上的两个动点,则AM+MP+PN的最小值为( )| A. | 2 | B. | 4sin40° | ||
| C. | 2$\sqrt{3}$ | D. | 4sin20°(1+cos20°+sin20°cos20°) |
分析 如图所示直线OC、y轴关于直线y=kx对称,直线OD、直线y=kx关于y轴对称,点A′是点A关于直线y=kx的对称点,作A′E⊥OD垂足为E,交y轴于点P,交直线y=kx于M,作PN⊥直线y=kx垂足为N,此时AM+PM+PN=A′M+PM+PE=A′E最小(垂线段最短),在RT△A′EO中利用勾股定理即可解决.
解答 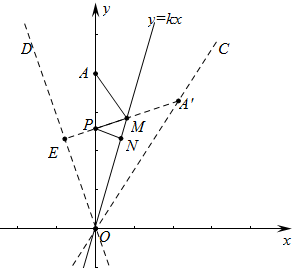 解:如图所示,直线OC、y轴关于直线y=kx对称,直线OD、直线y=kx关于y轴对称,点A′是点A关于直线y=kx的对称点.
解:如图所示,直线OC、y轴关于直线y=kx对称,直线OD、直线y=kx关于y轴对称,点A′是点A关于直线y=kx的对称点.
作A′E⊥OD垂足为E,交y轴于点P,交直线y=kx于M,作PN⊥直线y=kx垂足为N,
∵PN=PE,AM=A′M,
∴AM+PM+PN=A′M+PM+PE=A′E最小(垂线段最短),
在RT△A′EO中,∵∠A′EO=90°,OA′=4,∠A′OE=3∠AOM=60°,
∴OE=$\frac{1}{2}$OA′=2,A′E=$\sqrt{OA{′}^{2}-O{E}^{2}}$=$\sqrt{{4}^{2}-{2}^{2}}$=2$\sqrt{3}$.
∴AM+MP+PN的最小值为2$\sqrt{3}$.
故选C.
点评 本题考查轴对称-最短问题、垂线段最短、直角三角形30度角的性质、勾股定理等知识,解题的关键是利用轴对称性质正确找到等P的位置,题目有点难度,是最短问题中比较难的题目.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
17.下图中不能表示y是x的函数是( )
| A. |  | B. |  | C. |  | D. |  |
18.已知,圆锥的高h=$2\sqrt{3}$cm,底面半径r=2cm,则圆锥的侧面积为( )cm2.
| A. | 4$\sqrt{3}$π | B. | 8π | C. | 12π | D. | (4$\sqrt{3}$+4)π |
 已知:如图,在四边形ABCD中,AD∥BC,∠ABC=90°,点E是DC的中点,过点E作DC的垂线交AB于点P,交CB的延长线于点M,点F在线段ME上,且满足CF=AD,MF=MA.
已知:如图,在四边形ABCD中,AD∥BC,∠ABC=90°,点E是DC的中点,过点E作DC的垂线交AB于点P,交CB的延长线于点M,点F在线段ME上,且满足CF=AD,MF=MA.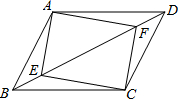 如图,已知E、F为平行四边形ABCD的对角线上的两点,且BE=DF,∠AEC=90°.求证:四边形AECF为矩形.
如图,已知E、F为平行四边形ABCD的对角线上的两点,且BE=DF,∠AEC=90°.求证:四边形AECF为矩形.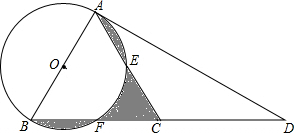 如图,在△ABC中,AC=BC,延长BC到点D,使CD=CB,连接AD,以AB为直径作⊙O,分别交AC、BC于点E、F
如图,在△ABC中,AC=BC,延长BC到点D,使CD=CB,连接AD,以AB为直径作⊙O,分别交AC、BC于点E、F