题目内容
 如图,在矩形ABCD中,点E是AD上一点,点F是AB上一点,EF=CE且EF⊥CE,求证:AE=AB.
如图,在矩形ABCD中,点E是AD上一点,点F是AB上一点,EF=CE且EF⊥CE,求证:AE=AB.考点:全等三角形的判定与性质,矩形的性质
专题:证明题
分析:根据矩形的性质,可得∠A=∠D=90°,AB=CD,根据余角的性质,可得∠AFE=∠DEC,根据全等三角形的判定与性质,可得AE与DC的关系,根据等量代换,可得答案.
解答:解:∵在矩形ABCD中
∴∠A=∠D=90°,AB=CD,
∴∠AEF+∠AFE=90°
∵EF⊥CE.
∴∠FEC=90°.
∴∠AEF+∠DEC=90°.
∴∠AFE=∠DEC.
在Rt△AEF与Rt△DCE中,
,
∴Rt△AEF≌Rt△DCE(AAS),
∴AE=CD.
∵AB=CD,
∴AE=AB.
∴∠A=∠D=90°,AB=CD,
∴∠AEF+∠AFE=90°
∵EF⊥CE.
∴∠FEC=90°.
∴∠AEF+∠DEC=90°.
∴∠AFE=∠DEC.
在Rt△AEF与Rt△DCE中,
|
∴Rt△AEF≌Rt△DCE(AAS),
∴AE=CD.
∵AB=CD,
∴AE=AB.
点评:本题考查了全等三角形的判定与性质,利用了矩形的性质,余角的性质,全等三角形的判定与性质.

练习册系列答案
相关题目
计算(27a4-9a3-15a2+81a)÷(-3a)的结果是( )
| A、-9a3-3a2-5a+27 |
| B、-9a3+3a2+5a-27 |
| C、-9a3-3a2+5a |
| D、-9a4+3a3+5a2-27a |
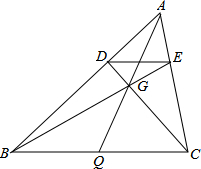 在△ABC中,作DE∥BC,连BE、CD交于一点G,连AG延长至BC上于Q.证明:Q是BC中点.
在△ABC中,作DE∥BC,连BE、CD交于一点G,连AG延长至BC上于Q.证明:Q是BC中点. 如图:已知AD∥BC,AD=CB,A、E、F、C在同一直线上且AE=CF,
如图:已知AD∥BC,AD=CB,A、E、F、C在同一直线上且AE=CF,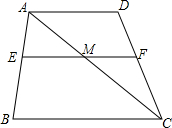 如图,在四边形ABCD中,AD∥BC∥EF,EF与AC相交于点M,已知
如图,在四边形ABCD中,AD∥BC∥EF,EF与AC相交于点M,已知 如图是一个正方体纸盒的两个侧面展开图,请你在其余三个正方体内分别填上适当的数,使得折成正方体后,相对的面上的两个数互为相反数.
如图是一个正方体纸盒的两个侧面展开图,请你在其余三个正方体内分别填上适当的数,使得折成正方体后,相对的面上的两个数互为相反数.