题目内容
8.解分式方程:(1)$\frac{4x}{x-2}=\frac{3}{2-x}+1$
(2)$\frac{x}{x+1}=1-\frac{2x-1}{{x}^{2}-1}$.
分析 两分式方程去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解.
解答 解:(1)去分母得:4x=-3+x-2,
移项合并得:3x=-5,
解得:x=-$\frac{5}{3}$,
经检验x=-$\frac{5}{3}$是分式方程的解;
(2)去分母得:x(x-1)=x2-1-2x+1,
整理得:x=0,
经检验x=0是分式方程的解.
点评 此题考查了解分式方程,解分式方程的基本思想是“转化思想”,把分式方程转化为整式方程求解.解分式方程一定注意要验根.

练习册系列答案
相关题目
3. 如图,下列各组条件中,不能判定△ABC≌△DEF的是( )
如图,下列各组条件中,不能判定△ABC≌△DEF的是( )
 如图,下列各组条件中,不能判定△ABC≌△DEF的是( )
如图,下列各组条件中,不能判定△ABC≌△DEF的是( )| A. | AB=DE,∠A=∠D,AC=DF | B. | ∠B=∠E,AB=DE,AC=DE | ||
| C. | ∠A=∠D,AB=DE,∠B=∠E | D. | AB=DE,BC=EF,AC=DF |
 已知:b是最小的正整数,且a,b满足(c-5)2+|a+b|=0,请回答问题:
已知:b是最小的正整数,且a,b满足(c-5)2+|a+b|=0,请回答问题: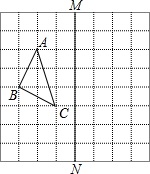 如图,在正方形网格中,每个小正方形的边长都为1,网格中有一个格点△ABC(即三角形的顶点都在格点上).
如图,在正方形网格中,每个小正方形的边长都为1,网格中有一个格点△ABC(即三角形的顶点都在格点上). 如图,AD⊥BC,垂足为点D,EF⊥BC,垂足为点F,且AD平分∠BAC,∠AGE与∠E相等吗?为什么?
如图,AD⊥BC,垂足为点D,EF⊥BC,垂足为点F,且AD平分∠BAC,∠AGE与∠E相等吗?为什么?
