题目内容
18. 已知:b是最小的正整数,且a,b满足(c-5)2+|a+b|=0,请回答问题:
已知:b是最小的正整数,且a,b满足(c-5)2+|a+b|=0,请回答问题:(1)请直接写出a、b、c的值.
a=-1 b=1 c=5.
(2)a、b、c所对应的点分别为A、B、C,点P为动点,其对应的数为x,当点P在数轴上什么位置时,P到A点的与P到B点的距离之和最小?C.
A.在A点时
B.在B点时
C.在AB之间(包括A,B两点)
D.在BC之间(包括B,C两点)
(3)在(1)(2)的条件下,点A、B、C开始在数轴上运动,若点A以每秒1个单位长度的速度向左运动,同时,点B和点C分别以每秒2个单位长度和5个单位长度的速度向右运动,假设t秒钟过后,若点B与点C之间的距离表示为BC,点A与点B之间的距离表示为AB.
请问:
BC-AB的值是否随着时间t的变化而变化?若变化,请说明理由:若不变,请求其值.
分析 (1)根据-1是最小正整和非负数的性质,即可解答;
(2)根据绝对值的几何意义,可得当点P在AB之间(包括A,B两点),P到A点与P到B点的距离之和最小;
(3)根据A,B,C的运动情况即可确定AB,BC的变化情况,即可确定AB-BC的值.
解答 解:(1)∵(c-5)2+|a+b|=0,b是最小的正整数,
∴c-5=0,b=1,a+b=0,
∴a=-1,b=1,c=5.
故答案为:-1,1,5;
(2)当点P在在AB之间(包括A,B两点)时,P到A点的与P到B点的距离之和最小.
故选:C.
(3)不变.
∵点A以每秒1个单位长度的速度向左运动,点B每秒2个单位长度向右运动,
∴A,B每秒钟增加3个单位长度;
∵点B和点C分别以每秒2个单位长度和5个单位长度的速度向右运动,
∴B,C每秒钟增加3个单位长度.
∴BC-AB=2,BC-AB的值不随着时间t的变化而改变.
点评 本题考查了数轴与绝对值,正确理解AB,BC的变化情况是关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
6.我国的陆地面积为9600000平方千米,9600000用科学记数法可表示为( )
| A. | 96×105 | B. | 9.6×106 | C. | 0.96×107 | D. | 960×104 |
13.新开通的万家丽快速桥全长约16500米,将16500用科学记数法表示为( )
| A. | 16.5×103 | B. | 1.65×104 | C. | 1.65×103 | D. | 0.165×104 |
3.下列四个图形中,轴对称图形的个数有( )


| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
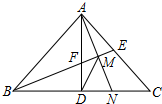 如图,等腰Rt△ABC中,∠BAC=90°,AD⊥BC于点D,∠ABC的平分线分别交AC、AD于E、F两点,M为EF的中点,AM的延长线交BC于点N,连接DM,下列结论:①DF=DN; ②△DMN为等腰三角形;③DM平分∠BMN;④AE=$\frac{2}{3}$EC;
如图,等腰Rt△ABC中,∠BAC=90°,AD⊥BC于点D,∠ABC的平分线分别交AC、AD于E、F两点,M为EF的中点,AM的延长线交BC于点N,连接DM,下列结论:①DF=DN; ②△DMN为等腰三角形;③DM平分∠BMN;④AE=$\frac{2}{3}$EC;