题目内容
1.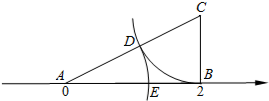 如图,在数轴上,点A、B表示的数分别为0、2,BC⊥AB于点B,且BC=1,连接AC,在AC上截取CD=BC,以A为圆心,AD的长为半径画弧,交线段AB于点E,则点E表示的实数是$\sqrt{5}$-1.
如图,在数轴上,点A、B表示的数分别为0、2,BC⊥AB于点B,且BC=1,连接AC,在AC上截取CD=BC,以A为圆心,AD的长为半径画弧,交线段AB于点E,则点E表示的实数是$\sqrt{5}$-1.
分析 根据垂直的定义得到∠ABC=90°,根据勾股定理得到AC=$\sqrt{A{B}^{2}+B{C}^{2}}$=$\sqrt{5}$,求得AD=AC-CD=$\sqrt{5}$-1,根据圆的性质得到AE=AD,即可得到结论.
解答 解:∵BC⊥AB,
∴∠ABC=90°,
∵AB=2,BC=1,
∴AC=$\sqrt{A{B}^{2}+B{C}^{2}}$=$\sqrt{5}$,
∵CD=BC,
∴AD=AC-CD=$\sqrt{5}$-1,
∵AE=AD,
∴AE=$\sqrt{5}$-1,
∴点E表示的实数是$\sqrt{5}$-1.
故答案为:$\sqrt{5}$-1.
点评 本题考查了勾股定理,实数与数轴,圆的性质,正确掌握勾股定理是解题的关键.

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
9.飞机在飞行过程中,如果上升23米记作“+23米”,那么下降15米应记作( )
| A. | -8米 | B. | +8米 | C. | -15米 | D. | +15米 |
16.下列各式计算正确的是( )
| A. | (a5)2=a7 | B. | 2x-2=$\frac{1}{2{x}^{2}}$ | C. | 3a2•2a3=6a5 | D. | a6÷a6=0 |
6.如果用-10%表示某商品的出口额比上一年减少10%,那么+12%则表示该商品的出口额比上一年( )
| A. | 增加2% | B. | 增加12% | C. | 减少12% | D. | 减少22% |
13.如果把分式$\frac{3x}{x+y}$中的x和y的值都扩大5倍,那么分式的值( )
| A. | 扩大5倍 | B. | 缩小5倍 | C. | 不改变; | D. | 扩大25倍 |
10.在Rt△ABC中,∠C=90°,BC=3,AB=4,则sinA的值为( )
| A. | $\frac{3}{5}$ | B. | $\frac{4}{5}$ | C. | $\frac{3}{4}$ | D. | $\frac{4}{3}$ |
 如图,矩形OABC与矩形ODEF是位似图形,P是位似中心,点B(4,2),E(-2,1),则点P的坐标为(-4,0).
如图,矩形OABC与矩形ODEF是位似图形,P是位似中心,点B(4,2),E(-2,1),则点P的坐标为(-4,0).