��Ŀ����
4����ͼ1����֪������y=-$\frac{\sqrt{3}}{3}$x2+$\frac{2\sqrt{3}}{3}$x+$\sqrt{3}$��x�ύ��A��B���㣨��A�ڵ�B����ࣩ����y�ύ�ڵ�C����D�ǵ�C���������߶Գ���ĶԳƵ㣬����CD������D��DH��x���ڵ�H������A��AE��AC��DH���ӳ����ڵ�E����1�����߶�DE�ij��ȣ�
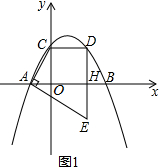
��2����ͼ2�������߶�AE����һ��F�����߶�DE����һ��P���ҵ�MΪֱ��PF�Ϸ��������ϵ�һ�㣬��CPF���ܳ���Сʱ����MPF��������ֵ�Ƕ��٣�
��3���ڣ�2���ʵ������£����õ��ġ�CFP��ֱ��AEƽ�Ƶõ���C��F��P�䣬����C��F��P����C��P�䷭�۵õ���C��P��F�壬����ƽ�ƹ����У�ֱ��F��P����x�ύ�ڵ�K�����Ƿ���������ĵ�K��ʹ�á�F��F��KΪ���������Σ����������OK��ֵ���������ڣ�˵�����ɣ�
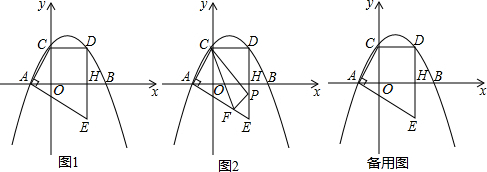
���� ��1�����ݽ���ʽ���C�����꣬�������D�����꣬�������DH�ij��ȣ���y=0�����A��B�����꣬Ȼ��֤�á�ACO�ס�EAH�����ݶ�Ӧ�߳ɱ������EH�ij������̶����DE�ij���
��2���ҵ�C����DE�ĶԳƵ�N��4��$\sqrt{3}$�����ҵ�C����AE�ĶԳƵ�G��-2��-$\sqrt{3}$��������GN����AE�ڵ�F����DE�ڵ�P����G��F��P��N�ĵ㹲��ʱ����CPF�ܳ�=CF+PF+CP=GF+PF+PN��С�����ݵ���������ֱ��GN�Ľ���ʽ��y=$\frac{\sqrt{3}}{3}$x-$\frac{\sqrt{3}}{3}$��ֱ��AE�Ľ���ʽ��y=-$\frac{\sqrt{3}}{3}$x-$\frac{\sqrt{3}}{3}$������M��y���ƽ���߽�FH�ڵ�Q�����M��m��-$\frac{\sqrt{3}}{3}$m2+$\frac{2\sqrt{3}}{3}$m+$\sqrt{3}$������Q��m��$\frac{\sqrt{3}}{3}$m-$\frac{\sqrt{3}}{3}$��������S��MFP=S��MQF+S��MQP���ó�S��MFP=-$\frac{\sqrt{3}}{3}$m2+$\frac{\sqrt{3}}{3}$m+$\frac{4}{3}$$\sqrt{3}$�����ݽ���ʽ������ã���MPF��������ֵ��
��3���ɣ�2����֪C��0��$\sqrt{3}$����F��0��$\frac{\sqrt{3}}{3}$����P��2��$\frac{\sqrt{3}}{3}$�������CF=$\frac{4\sqrt{3}}{3}$��CP=$\frac{4\sqrt{3}}{3}$�������ó���CFPΪ�ȱ������Σ��߳�Ϊ$\frac{4\sqrt{3}}{3}$������֮���γɱ߳�Ϊ$\frac{4\sqrt{3}}{3}$������C��F��P��F�壬��F��F��=4��Ȼ����������������ü��ɣ�
���  �⣺��1������������y=-$\frac{\sqrt{3}}{3}$x2+$\frac{2\sqrt{3}}{3}$x+$\sqrt{3}$��
�⣺��1������������y=-$\frac{\sqrt{3}}{3}$x2+$\frac{2\sqrt{3}}{3}$x+$\sqrt{3}$��
��x=0����y=$\sqrt{3}$����C��0��$\sqrt{3}$����D��2��$\sqrt{3}$����
��DH=$\sqrt{3}$��
��y=0����-$\frac{\sqrt{3}}{3}$x2+$\frac{2\sqrt{3}}{3}$x+$\sqrt{3}$=0����x1=-1��x2=3��
��A��-1��0����B��3��0����
��AE��AC��EH��AH��
���ACO�ס�EAH��
��$\frac{OC}{AH}$=$\frac{OA}{EH}$����$\frac{\sqrt{3}}{3}$=$\frac{1}{EH}$��
��ã�EH=$\sqrt{3}$��
��DE=2$\sqrt{3}$��
��2���ҵ�C����DE�ĶԳƵ�N��4��$\sqrt{3}$�����ҵ�C����AE�ĶԳƵ�G��-2��-$\sqrt{3}$����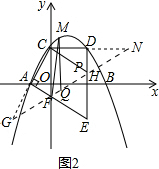
����GN����AE�ڵ�F����DE�ڵ�P����G��F��P��N�ĵ㹲��ʱ����CPF�ܳ�=CF+PF+CP=GF+PF+PN��С��
ֱ��GN�Ľ���ʽ��y=$\frac{\sqrt{3}}{3}$x-$\frac{\sqrt{3}}{3}$��ֱ��AE�Ľ���ʽ��y=-$\frac{\sqrt{3}}{3}$x-$\frac{\sqrt{3}}{3}$��
�����ã�F ��0��-$\frac{\sqrt{3}}{3}$����P��2��$\frac{\sqrt{3}}{3}$����
����M��y���ƽ���߽�FH�ڵ�Q��
���M��m��-$\frac{\sqrt{3}}{3}$m2+$\frac{2\sqrt{3}}{3}$m+$\sqrt{3}$������Q��m��$\frac{\sqrt{3}}{3}$m-$\frac{\sqrt{3}}{3}$������0��m��2����
��S��MFP=S��MQF+S��MQP=$\frac{1}{2}$MQ��2=MQ=-$\frac{\sqrt{3}}{3}$m2+$\frac{\sqrt{3}}{3}$m+$\frac{4}{3}$$\sqrt{3}$��
�߶Գ���Ϊ��ֱ��m=$\frac{1}{2}$��2���������£�
��m=$\frac{1}{2}$ʱ����MPF��������ֵ��$\frac{17}{12}$$\sqrt{3}$��
��3���ɣ�2����֪C��0��$\sqrt{3}$����F��0��$\frac{\sqrt{3}}{3}$����P��2��$\frac{\sqrt{3}}{3}$����
��CF=$\frac{4\sqrt{3}}{3}$��CP=$\sqrt{C{D}^{2}+D{P}^{2}}$=$\frac{4\sqrt{3}}{3}$��
��OC=$\sqrt{3}$��OA=1��
���OCA=30�㣬
��FC=FG��
���OCA=��FGA=30�㣬
���CFP=60�㣬
���CFPΪ�ȱ������Σ��߳�Ϊ$\frac{4\sqrt{3}}{3}$��
����֮���γɱ߳�Ϊ$\frac{4\sqrt{3}}{3}$������C��F��P��F�壬��F��F��=4��
1����K F��=KF��ʱ����ͼ3��
��K��F��F��Ĵ�ֱƽ�����ϣ�����K��B�غϣ�����Ϊ��3��0����
��OK=3��
2����F��F��=F��Kʱ����ͼ4��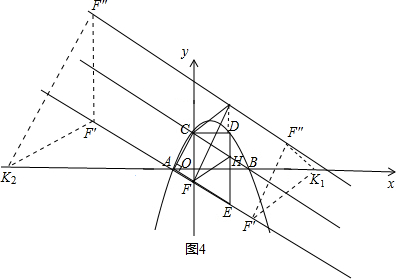
��F��F��=F��K=4��
��FP�Ľ���ʽΪ��y=$\frac{\sqrt{3}}{3}$x-$\frac{\sqrt{3}}{3}$��
����ƽ�ƹ����У�F��K��x��ļн�Ϊ30�㣬
�ߡ�OAF=30�㣬
��F��K=F��A
��AK=4$\sqrt{3}$
��OK=4$\sqrt{3}$-1����4$\sqrt{3}$+1��
3����F��F��=F��Kʱ����ͼ5��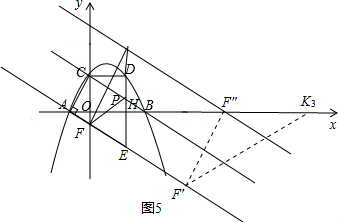
����ƽ�ƹ����У�F��F��ʼ����x��н�Ϊ60�㣬
�ߡ�OAF=30�㣬
���AF��F��=90�㣬
��F��F��=F��K=4��
��AF��=8��
��AK=12��
��OK=11��
����������OK=3��4$\sqrt{3}$-1��4$\sqrt{3}$+1����11��
���� �����Ƕ��κ������ۺ��⣬�����˶��κ����Ľ���ʹ���ϵ��������κ����Ľ���ʽ�Լ���ֵ���⣬���������������Ƶ��ж������ʣ��ȱ������ε��ж������ʣ����������ε����ʵȣ��������۵�˼���ǽ���Ĺؼ���

 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�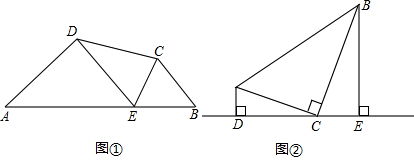
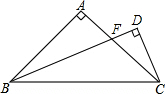 ��ͼ����֪����ֱ��������ABC�У�AB=AC����BAC=90�㣬BFƽ�֡�ABC��CD��BD��BF���ӳ����ڵ�D����˵����BF=2CD��
��ͼ����֪����ֱ��������ABC�У�AB=AC����BAC=90�㣬BFƽ�֡�ABC��CD��BD��BF���ӳ����ڵ�D����˵����BF=2CD��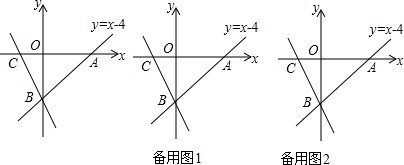
 ��ͼ����֪��ƽ��ֱ������ϵxOy�У�O������ԭ�㣬������y=-x2+2mx+n��m��0��n��0���Ķ���ΪD����y��Ľ���ΪC������C��CA��x�ύ�������ڵ�A����AC�ӳ�����ȡ��B��ʹBC=$\frac{1}{2}$AC������OA��OB��BD��AD��
��ͼ����֪��ƽ��ֱ������ϵxOy�У�O������ԭ�㣬������y=-x2+2mx+n��m��0��n��0���Ķ���ΪD����y��Ľ���ΪC������C��CA��x�ύ�������ڵ�A����AC�ӳ�����ȡ��B��ʹBC=$\frac{1}{2}$AC������OA��OB��BD��AD��