题目内容
12.已知关于x的方程(1-2k)x2-2$\sqrt{k+1}$x-1=0有实数根,则k的取值范围是( )| A. | k≥2 | B. | k≤2 | C. | -1≤k≤2 | D. | -1≤k≤2且$k≠\frac{1}{2}$ |
分析 根据方程有实根得出△≥0,求出不等式的解集,结合二次根式的意义求得答案即可.
解答 解:当1-2k=0时,(1-2k)x2-2$\sqrt{k+1}$x-1=0变为-$\sqrt{6}$x-1=0,
此时方程有实数根;
当1-2k≠0时,
由题意知,△=4(k+1)+4(1-2k)≥0,且k+1≥0,
∴-1≤k≤2.
∴当-1≤k≤2时,关于x的方程(1-2k)x2-2$\sqrt{k+1}$x-1=0有实数根.
故选:C.
点评 此题考查一元二次方程根的情况与判别式△的关系:(1)△>0?方程有两个不相等的实数根;(2)△=0?方程有两个相等的实数根;(3)△<0?方程没有实数根.

练习册系列答案
相关题目
20.已知一个圆锥的底面直径为6cm,母线长为10cm,则这个圆锥的侧面积为( )
| A. | 15πcm2 | B. | 30πcm2 | C. | 60πcm2 | D. | 3$\sqrt{91}$cm2 |
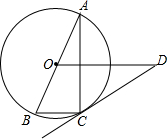 已知:如图,AB是⊙O的直径,BC是⊙O的弦,点D是⊙O外一点,∠DCA=∠B.
已知:如图,AB是⊙O的直径,BC是⊙O的弦,点D是⊙O外一点,∠DCA=∠B.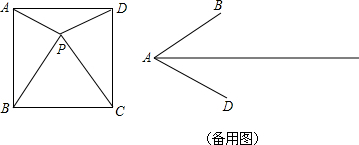
 如图,在△ABC中,∠ACB=90°,AB=5,AC=4,过点C作直线MC使得∠BCM=∠BAC,求点B到直线MC的距离.
如图,在△ABC中,∠ACB=90°,AB=5,AC=4,过点C作直线MC使得∠BCM=∠BAC,求点B到直线MC的距离.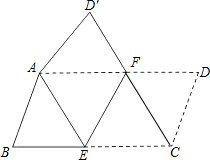 如图,将平行四边形纸片ABCD按如图方式折叠,使点C与点A重合,点D的落点记为点D′,折痕为EF,连接CF.
如图,将平行四边形纸片ABCD按如图方式折叠,使点C与点A重合,点D的落点记为点D′,折痕为EF,连接CF. 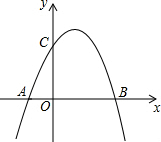 如图,二次函数y=ax2+bx+c的图象交x轴于A(-1,0),B(2,0),交y轴于C(0,2),作直线BC.
如图,二次函数y=ax2+bx+c的图象交x轴于A(-1,0),B(2,0),交y轴于C(0,2),作直线BC.