题目内容
16．
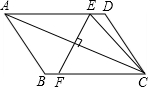如图，在?ABCD中，对角线AC的垂直平分线分别交AD、BC于点E、F，连接CE，若△CED的周长为6，则?ABCD的周长为（ ）| A． | 6 | B． | 12 | C． | 18 | D． | 24 |
分析 由平行四边形的性质得出DC=AB，AD=BC，由线段垂直平分线的性质得出AE=CE，得出△CDE的周长=AD+DC，即可得出结果．
解答 解：∵四边形ABCD是平行四边形，
∴DC=AB，AD=BC，
∵AC的垂直平分线交AD于点E，
∴AE=CE，
∴△CDE的周长=DE+CE+DC=DE+AE+DC=AD+DC=6，
∴?ABCD的周长=2×6=12；
故选：B．
点评 本题考查了平行四边形的性质、线段垂直平分线的性质、三角形周长的计算；熟练掌握平行四边形的性质，并能进行推理计算是解决问题的关键．
练习册系列答案
阅读快车系列答案
相关题目
如图中，AB∥EF∥CD，∠ABC=46°，CE平分∠BCD，则∠CEF等于157°．
7．若不等式组$\left\{\begin{array}{l}{x≥-b}\\{1-2x＞x-2}\end{array}\right.$无解，则实数b的取值范围是（ ）
| A． | b≤-1 | B． | b≥-1 | C． | b＜-1 | D． | b＞-1 |
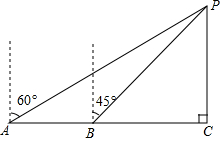一艘货轮由西向东航行，在A处测得灯塔P在它的北偏东60°方向，继续航行到达B处，测得灯塔P在它的东北方向，若灯塔P正南方向4海里的C处是港口，点A，B，C在一条直线上，则这艘货轮由A到B航行的路程为（4$\sqrt{3}$-4）海里（结果保留根号）．
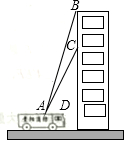贵阳市某消防支队在一幢居民楼前进行消防演习，如图所示，消防官兵利用云梯成功救出在C处的求救者后，发现在C处正上方17米的B处又有一名求救者，消防官兵立刻升高云梯将其救出，已知点A与居民楼的水平距离是15米，且在A点测得第一次施救时云梯与水平线的夹角∠CAD=60°，求第二次施救时云梯与水平线的夹角∠BAD的度数（结果精确到1°）．
8．下列四组线段中，不能作为直角三角形三条边的是（ ）
| A． | 3cm，4cm，5cm | B． | 2cm，2cm，2$\sqrt{2}$cm | C． | 2cm，5cm，6cm | D． | 5cm，12cm，13cm |