题目内容
7.若不等式组$\left\{\begin{array}{l}{x≥-b}\\{1-2x>x-2}\end{array}\right.$无解,则实数b的取值范围是( )| A. | b≤-1 | B. | b≥-1 | C. | b<-1 | D. | b>-1 |
分析 根据解一元一次不等式组的方法可以分别求得两个不等式的解集,再根据不等式组$\left\{\begin{array}{l}{x≥-b}\\{1-2x>x-2}\end{array}\right.$无解,从而可以求得b的取值范围.
解答 解:由不等式组$\left\{\begin{array}{l}{x≥-b}\\{1-2x>x-2}\end{array}\right.$得,$\left\{\begin{array}{l}{x≥-b}\\{x<1}\end{array}\right.$,
∵不等式组$\left\{\begin{array}{l}{x≥-b}\\{1-2x>x-2}\end{array}\right.$无解,
∴-b≥1,
解得,b≤-1,
故选A.
点评 本题考查解一元一次不等式组,解答本题的关键是明确解一元一次不等式的方法,找准对应关系.

练习册系列答案
相关题目
17.若a<b,那么下列结论中正确的是( )
| A. | a-3>b-3 | B. | 3a>3b | C. | $\frac{a}{3}$>$\frac{b}{3}$ | D. | -3a>-3b |
18.如果关于x的不等式2≤3x+b<8的整数解之和为7,那么b的取值范围是( )
| A. | -7≤b≤-4 | B. | -7<b<-4 | C. | -7<b≤-4 | D. | -7≤b<-4 |
15.x与$\frac{2}{3}$的差的一半是正数,用不等式表示为( )
| A. | $\frac{1}{2}$(x-$\frac{2}{3}$)<0 | B. | $\frac{1}{2}$x-$\frac{2}{3}$<0 | C. | $\frac{1}{2}$x-$\frac{2}{3}>$0 | D. | $\frac{1}{2}$(x-$\frac{2}{3}$)>0 |
14.下列四个数中,最小的数是( )
| A. | -1 | B. | 2 | C. | 0 | D. | -$\sqrt{3}$ |
 如图:正方形ABCD中,E是对角线AC上的一点,若∠CED=70°,则∠ABE的度数是25°.
如图:正方形ABCD中,E是对角线AC上的一点,若∠CED=70°,则∠ABE的度数是25°.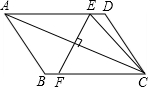 如图,在?ABCD中,对角线AC的垂直平分线分别交AD、BC于点E、F,连接CE,若△CED的周长为6,则?ABCD的周长为( )
如图,在?ABCD中,对角线AC的垂直平分线分别交AD、BC于点E、F,连接CE,若△CED的周长为6,则?ABCD的周长为( )