题目内容
12．计算：（1）（-$\frac{2{a}^{2}b}{3c}$）2
（2）$\frac{2a}{5{a}^{2}b}$+$\frac{3b}{10a{b}^{2}}$
（3）（a+$\frac{1}{a-2}$）÷（1+$\frac{1}{a-2}$）
分析 （1）原式分子分母分别乘方即可得到结果；
（2）原式通分并利用同分母分式的加法法则计算即可得到结果；
（3）原式括号中两项通分并利用同分母分式的加法法则计算，同时利用除法法则变形，约分即可得到结果．
解答 解：（1）原式=$\frac{4{a}^{4}{b}^{2}}{9{c}^{2}}$；
（2）原式=$\frac{4ab+3ab}{10{a}^{2}{b}^{2}}$=$\frac{7ab}{10{a}^{2}{b}^{2}}$=$\frac{7}{10ab}$；
（3）原式=$\frac{{a}^{2}-2a+1}{a-2}$÷$\frac{a-2+1}{a-2}$=$\frac{（a-1）^{2}}{a-2}$•$\frac{a-2}{a-1}$=a-1．
点评 此题考查了分式的混合运算，熟练掌握运算法则是解本题的关键．
练习册系列答案
相关题目
用18m长的铝合金型材做一个形状如图所示的矩形窗框．做成长、宽各为多少时，才能使做成的窗框的透光面积最大？最大透光面积是多少？
7．从分别标有号数1到10的10张卡片中，随意抽取一张，其号数为3的倍数的概率是（ ）
| A． | $\frac{7}{10}$ | B． | $\frac{1}{2}$ | C． | $\frac{3}{10}$ | D． | $\frac{1}{10}$ |
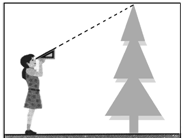小莉站在离一棵树水平距离为2米的地方，用一块含30°的直角三角板按如图所示的方式测量这棵树的高度，已知小莉的眼睛离地面的高度是1.5米，那么她测得这棵树的高度为（$\frac{2\sqrt{3}}{3}$+1.5）米．（结果保留根号）