题目内容
 已知:如图所示,在平行四边形ABCD中,P为CD的中点,AP的延长线交BC的延长线于E,PQ∥CE交DE于点Q.
已知:如图所示,在平行四边形ABCD中,P为CD的中点,AP的延长线交BC的延长线于E,PQ∥CE交DE于点Q.求证:PQ=
| 1 |
| 2 |
考点:平行四边形的性质,三角形中位线定理
专题:证明题
分析:利用已知条件可证明△ADP≌△ECP,从而证明AD=CE,因为AD=BC,所以BC=AD=CE,再利用三角形的中位线定理即可证明PQ=
BC.
| 1 |
| 2 |
解答:证明:∵四边形ABCD为平行四边形,
∵AD=BC,AD∥BC,
∴∠ADP=∠ECP,
∵P为CD的中点,
∴AP=EP,
∵∠APD=∠EPC,
∴△ADP≌△ECP,
∴AD=CE,
∴BC=CE,
∵PQ∥CE交DE于点Q,
∴PQ=
CE,
∴PQ=
BC.
∵AD=BC,AD∥BC,
∴∠ADP=∠ECP,
∵P为CD的中点,
∴AP=EP,
∵∠APD=∠EPC,
∴△ADP≌△ECP,
∴AD=CE,
∴BC=CE,
∵PQ∥CE交DE于点Q,
∴PQ=
| 1 |
| 2 |
∴PQ=
| 1 |
| 2 |
点评:本题考查了平行四边形的性质、全等三角形的判定和全等三角形的性质以及三角形的中位线定理:三角形的中位线平行于第三边,并且等于第三边的一半.

练习册系列答案
相关题目
下列运算正确的是( )
| A、a6÷a2=a3 |
| B、(a2)3=a8 |
| C、(a2b)3=a6b3 |
| D、a2•a3=a6 |
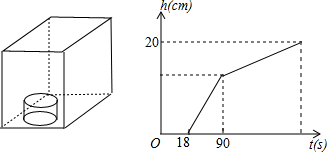 .水槽中水面上升的高度h与注水时间t之间的函数关系如图所示.
.水槽中水面上升的高度h与注水时间t之间的函数关系如图所示.  到琴弦.(答案需为整数)
到琴弦.(答案需为整数)