题目内容
12.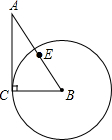 如图,在△ABC中,∠C=90°,BC=3cm,AC=4cm
如图,在△ABC中,∠C=90°,BC=3cm,AC=4cm(1)以B为圆心,BC为半径画⊙B,点A、C及AB的中点E与⊙B有怎样的位置关系?
(2)以A为圆心,R为半径画⊙A,若B、C、E三点中至少有一点在圆内,至少有一点在圆外,则⊙A的半径R应满足什么条件?
分析 (1)先根据勾股定理求出AB的长,再由点E时AB的中点即可得出结论;
(2)根据AE,AC及AB的长即可得出结论.
解答 解:(1)∵在△ABC中,∠C=90°,BC=3cm,AC=4cm,
∴AB=$\sqrt{{3}^{2}+{4}^{2}}$=5cm.
∵点E是线段AB的中点,
∴BE=$\frac{5}{2}$cm<3cm,
∴点E在圆内,点B在圆上,点A在圆外;
(2)∵AB=5cm,
∴AE=$\frac{5}{2}$cm,
∵AC=4cm,
∴若B、C、E三点中至少有一点在圆内,则$\frac{5}{2}$cm<r<5cm.
点评 本题考查的是点与圆的位置关系,熟知点与圆的三种位置关系是解答此题的关键.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
2.l00米长的小棒,第1次截去一半,第2次截去剩下的$\frac{1}{3}$,第三次截去剩下的$\frac{1}{4}$,如此下去,直到截去剩下的$\frac{1}{100}$,则剩下的小棒长为( )米.
| A. | 20 | B. | 15 | C. | 1 | D. | 50 |
3.把(-5)-(+7)+(-3)+(-11)写成省略加号的代数和的形式,正确的是( )
| A. | -5+7-3-11 | B. | (-5)(+7)(-3)(-11) | C. | -5-7-3-11 | D. | -5-7+-3+11 |
2.下列运算中,正确的是( )
| A. | $\root{6}{(a-b)^{6}}$=a-b | B. | $\root{8}{({a}^{2}+{b}^{2})^{8}}={a}^{2}+{b}^{2}$ | ||
| C. | $\root{4}{{a}^{4}}$-$\root{4}{{b}^{4}}$=a-b | D. | $\root{10}{(a+b)^{10}}$=a+b |
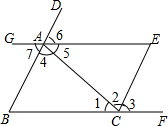 如图,由哪些条件,可得到直线AE∥BF,AB∥CE,直接写出这个条件,不写理由.
如图,由哪些条件,可得到直线AE∥BF,AB∥CE,直接写出这个条件,不写理由.
 如图所示,直线AB、CD被直线EF所截,若∠1=∠2,则AB∥CD;若∠3=∠2,则AB∥CD;若∠2+∠4=180°,则AB∥CD.
如图所示,直线AB、CD被直线EF所截,若∠1=∠2,则AB∥CD;若∠3=∠2,则AB∥CD;若∠2+∠4=180°,则AB∥CD. 如图,已知在△ABC中,AD平分∠BAC,BE∥AD,交CA延长线交于点E,F是BE的中点,求证:AF⊥BE.
如图,已知在△ABC中,AD平分∠BAC,BE∥AD,交CA延长线交于点E,F是BE的中点,求证:AF⊥BE.