Question

【题目】某商场用两个月时间试销某种新型商品，经市场调查，该商品的第天的进价(元／件)与(天)之间的相关信息如下表：

时间(天)
进价(元／件)		40

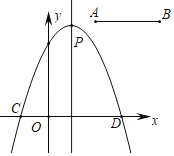
该商品在销售过程中，销售量(件)与(天)之间的函数关系如图所示：

在销售过程中，商场每天销售的该产品以每件80元的价格全部售出．

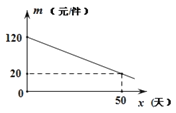
（1）求该商品的销售量(件)与(天)之间的函数关系；

（2）设第天该商场销售该商品获得的利润为元，求出与之间的函数关系式，并求出第几天销售利润最大，最大利润是多少元？

（3）在销售过程中，当天的销售利润不低于2400元的共有多少天？

Answer 1

【答案】（1）；（2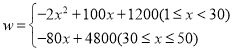），第25天时利润最大，最大利润为2450元；（3）共有11天的销售利润不低于2400元．

【解析】

（1）利用待定系数法求解即可；

（2）分和两种情况，分别根据“利润（售价进价）销售量”建立函数关系式，然后利用一次函数和二次函数的性质求解即可；

（3）根据（2）的结论，分别利用一次函数和二次函数的性质求出x的取值范围，再找出符合条件的整数即可．

（1）设该商品的销售量与之间的函数关系为

由图可知，点，在上

将点，代入得

解得

则该商品的销售量与之间的函数关系为；

（2）由题意，分以下两种情况：

①当时

由二次函数的性质可知，当时，取得最大值，最大值为2450

②当时

∵

∴随的增大而减小

则当时，取得最大值，最大值为

因

故第25天时利润最大，最大利润为2450元

综上，与之间的函数关系式为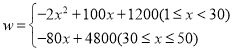，第25天时利润最大，最大利润为2450元；

（3）①当时，

则

∴或

∴，利润不低于2400元

即此时，共有10天的销售利润不低于2400元

②当时，

则

解得

即此时，只有1天的销售利润不低于2400元

综上，共有11天的销售利润不低于2400元．