题目内容
【题目】将一段抛物线![]() 向右依次平移3个单位,得到第2,3,4段抛物线,设这四段抛物线分别为
向右依次平移3个单位,得到第2,3,4段抛物线,设这四段抛物线分别为![]() ,若直线
,若直线![]() 与第四段抛物线
与第四段抛物线![]() 有唯一公共点,则
有唯一公共点,则![]() 的取值范围是( )
的取值范围是( )
A.![]() B.
B.![]() C.
C.![]() 或
或![]() D.
D.![]()
【答案】C
【解析】
根据平移求出抛物线![]() 的解析式,然后当直线与
的解析式,然后当直线与![]() 相切时通过联立方程求出此时b的值,
相切时通过联立方程求出此时b的值,
再分别求出当直线经过点(9,0)和(12,0)时的b的值,进而可求得符合题意的b的取值范围.
解:由题意得,抛物线![]() 是由抛物线
是由抛物线![]() 向右平移9个单位得到的,
向右平移9个单位得到的,
∴抛物线![]() 的解析式为:
的解析式为:![]()
当直线![]() 与抛物线
与抛物线![]() 相切时,
相切时,
则联立方程![]() 且该方程有两个相等的实数根,
且该方程有两个相等的实数根,
整理得![]() ,
,
∴![]() ,
,
解得:![]() ,
,
∵抛物线![]() 的解析式为:
的解析式为:![]()
∴当y=0时,则x1=9,x2=12,
∴抛物线![]() 与x轴的交点坐标为:(9,0),(12,0),
与x轴的交点坐标为:(9,0),(12,0),
∴当直线![]() 经过(9,0)时,
经过(9,0)时,![]() ,
,
则![]() ,
,
当直线![]() 经过(12,0)时,
经过(12,0)时,![]() ,
,
则![]() ,
,
∵直线![]() 与抛物线
与抛物线![]() 有唯一公共点,
有唯一公共点,
∴![]() 的取值范围是
的取值范围是![]() 或
或![]() ,
,
故选:C.

练习册系列答案
相关题目
【题目】某商场用两个月时间试销某种新型商品,经市场调查,该商品的第![]() 天的进价
天的进价![]() (元/件)与
(元/件)与![]() (天)之间的相关信息如下表:
(天)之间的相关信息如下表:
时间 |
|
|
进价 |
| 40 |
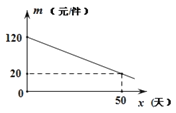
该商品在销售过程中,销售量![]() (件)与
(件)与![]() (天)之间的函数关系如图所示:
(天)之间的函数关系如图所示:
在销售过程中,商场每天销售的该产品以每件80元的价格全部售出.
(1)求该商品的销售量![]() (件)与
(件)与![]() (天)之间的函数关系;
(天)之间的函数关系;
(2)设第![]() 天该商场销售该商品获得的利润为
天该商场销售该商品获得的利润为![]() 元,求出
元,求出![]() 与
与![]() 之间的函数关系式,并求出第几天销售利润最大,最大利润是多少元?
之间的函数关系式,并求出第几天销售利润最大,最大利润是多少元?
(3)在销售过程中,当天的销售利润不低于2400元的共有多少天?