题目内容
15.观察下列图形规律:当n=5时,图形“●”的个数和“△”的个数相等.
分析 首先根据n=1、2、3、4时,“●”的个数分别是3、6、9、12,判断出第n个图形中“●”的个数是3n;然后根据n=1、2、3、4,“△”的个数分别是1、3、6、10,判断出第n个“△”的个数是$\frac{n(n+1)}{2}$;最后根据图形“●”的个数和“△”的个数相等,求出n的值是多少即可.
解答 解:∵n=1时,“●”的个数是3=3×1;
n=2时,“●”的个数是6=3×2;
n=3时,“●”的个数是9=3×3;
n=4时,“●”的个数是12=3×4;
∴第n个图形中“●”的个数是3n;
又∵n=1时,“△”的个数是1=$\frac{1×(1+1)}{2}$;
n=2时,“△”的个数是3=$\frac{2×(2+1)}{2}$;
n=3时,“△”的个数是6=$\frac{3×(3+1)}{2}$;
n=4时,“△”的个数是10=$\frac{4×(4+1)}{2}$;
∴第n个“△”的个数是$\frac{n(n+1)}{2}$;
由3n=$\frac{n(n+1)}{2}$,
可得n2-5n=0,
解得n=5或n=0(舍去),
∴当n=5时,图形“●”的个数和“△”的个数相等.
故答案为:5.
点评 此题主要考查了规律型:图形的变化类问题,要熟练掌握,解答此类问题的关键是:首先应找出图形哪些部分发生了变化,是按照什么规律变化的,通过分析找到各部分的变化规律后直接利用规律求解.探寻规律要认真观察、仔细思考,善用联想来解决这类问题.

练习册系列答案
相关题目
20.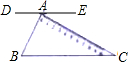 如图,一块含30°角的直角三角板ABC的直角顶点A在直线DE上,且BC∥DE,则∠CAE等于( )
如图,一块含30°角的直角三角板ABC的直角顶点A在直线DE上,且BC∥DE,则∠CAE等于( )
 如图,一块含30°角的直角三角板ABC的直角顶点A在直线DE上,且BC∥DE,则∠CAE等于( )
如图,一块含30°角的直角三角板ABC的直角顶点A在直线DE上,且BC∥DE,则∠CAE等于( )| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
7.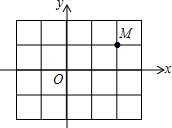 如图,在平面直角坐标系中,将点M(2,1)向下平移2个单位长度得到点N,则点N的坐标为( )
如图,在平面直角坐标系中,将点M(2,1)向下平移2个单位长度得到点N,则点N的坐标为( )
 如图,在平面直角坐标系中,将点M(2,1)向下平移2个单位长度得到点N,则点N的坐标为( )
如图,在平面直角坐标系中,将点M(2,1)向下平移2个单位长度得到点N,则点N的坐标为( )| A. | (2,-1) | B. | (2,3) | C. | (0,1) | D. | (4,1) |
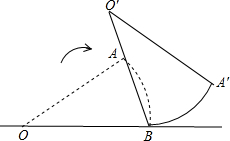 如图,已知扇形AOB中,OA=10cm,∠AOB=36°.
如图,已知扇形AOB中,OA=10cm,∠AOB=36°.
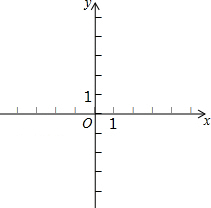 在平面直角坐标系xOy中,过点(0,2)且平行于x轴的直线,与直线y=x-1交于点A,点A关于直线x=1的对称点为B,抛物线C1:y=x2+bx+c经过点A,B.
在平面直角坐标系xOy中,过点(0,2)且平行于x轴的直线,与直线y=x-1交于点A,点A关于直线x=1的对称点为B,抛物线C1:y=x2+bx+c经过点A,B.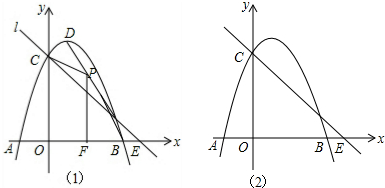
 如图,四边形ABCD中,∠A=∠ABC=90°,AD=1,BC=3,E是边CD的中点,连接BE并延长与AD的延长线相交于点F.
如图,四边形ABCD中,∠A=∠ABC=90°,AD=1,BC=3,E是边CD的中点,连接BE并延长与AD的延长线相交于点F.