题目内容
20. 在平面直角坐标系xOy中,过点(0,2)且平行于x轴的直线,与直线y=x-1交于点A,点A关于直线x=1的对称点为B,抛物线C1:y=x2+bx+c经过点A,B.
在平面直角坐标系xOy中,过点(0,2)且平行于x轴的直线,与直线y=x-1交于点A,点A关于直线x=1的对称点为B,抛物线C1:y=x2+bx+c经过点A,B.(1)求点A,B的坐标;
(2)求抛物线C1的表达式及顶点坐标;
(3)若抛物线C2:y=ax2(a≠0)与线段AB恰有一个公共点,结合函数的图象,求a的取值范围.
分析 (1)当y=2时,则2=x-1,解得x=3,确定A(3,2),根据AB关于x=1对称,所以B(-1,2).
(2)把(3,2),(-1,2)代入抛物线C1:y=x2+bx+c得$\left\{\begin{array}{l}{2=9+3b+c}\\{2=1-b+c}\end{array}\right.$,求出b,c的值,即可解答;
(3)画出函数图象,把A,B代入y=ax2,求出a的值,即可解答.
解答 解:(1)当y=2时,则2=x-1,
解得:x=3,
∴A(3,2),
∵点A关于直线x=1的对称点为B,
∴B(-1,2).
(2)把(3,2),(-1,2)代入抛物线C1:y=x2+bx+c得:
$\left\{\begin{array}{l}{2=9+3b+c}\\{2=1-b+c}\end{array}\right.$
解得:$\left\{\begin{array}{l}{b=-2}\\{c=-1}\end{array}\right.$
∴y=x2-2x-1.
顶点坐标为(1,-2).
(3)如图,当C2过A点,B点时为临界,
代入A(3,2)则9a=2,
解得:a=$\frac{2}{9}$,
代入B(-1,2),则a(-1)2=2,
解得:a=2,
∴$\frac{2}{9}≤a<2$.
点评 本题考查了二次函数的性质,解集本题的关键是求出二次函数的解析式,并结合图形解决问题.

练习册系列答案
 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案
相关题目
5. 如图,已知经过原点的抛物线y=ax2+bx+c(a≠0)的对称轴是直线x=-1,下列结论中:?
如图,已知经过原点的抛物线y=ax2+bx+c(a≠0)的对称轴是直线x=-1,下列结论中:?
①ab>0,?②a+b+c>0,?③当-2<x<0时,y<0.
正确的个数是( )
 如图,已知经过原点的抛物线y=ax2+bx+c(a≠0)的对称轴是直线x=-1,下列结论中:?
如图,已知经过原点的抛物线y=ax2+bx+c(a≠0)的对称轴是直线x=-1,下列结论中:?①ab>0,?②a+b+c>0,?③当-2<x<0时,y<0.
正确的个数是( )
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
5.来宾市辖区面积约为13400平方千米,这一数字用科学记数法表示为( )
| A. | 1.34×102 | B. | 1.34×103 | C. | 1.34×104 | D. | 1.34×105 |
12.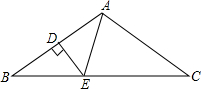 如图,在△ABC中,AB=AC,∠BAC=100°,AB的垂直平分线DE分别交AB、BC于点D、E,则∠BAE=( )
如图,在△ABC中,AB=AC,∠BAC=100°,AB的垂直平分线DE分别交AB、BC于点D、E,则∠BAE=( )
 如图,在△ABC中,AB=AC,∠BAC=100°,AB的垂直平分线DE分别交AB、BC于点D、E,则∠BAE=( )
如图,在△ABC中,AB=AC,∠BAC=100°,AB的垂直平分线DE分别交AB、BC于点D、E,则∠BAE=( )| A. | 80° | B. | 60° | C. | 50° | D. | 40° |
9.老师想知道学生每天上学路上要花多少时间,于是让大家将每天来校的单程时间写在纸上用于统计.下面是全班30名学生单程所花时间(单位:分)与对应人数(单位:人)的统计表,则关于这30名学生单程所花时间的数据,下列结论正确的是( )
| 单程所花时间 | 5 | 10 | 15 | 20 | 25 | 30 | 35 | 45 |
| 人数 | 3 | 3 | 6 | 12 | 2 | 2 | 1 | 1 |
| A. | 众数是12 | B. | 平均数是18 | C. | 极差是45 | D. | 中位数是20 |
10.$\frac{1}{2}$的倒数为( )
| A. | -2 | B. | -$\frac{1}{2}$ | C. | $\frac{1}{2}$ | D. | 2 |
 如图,已知AB是⊙O的直径,EA是⊙O的切线,A为切点,D是EA上一点,且∠ABD=30°,DB交⊙O于点C,连结OC并延长交EA于点P.
如图,已知AB是⊙O的直径,EA是⊙O的切线,A为切点,D是EA上一点,且∠ABD=30°,DB交⊙O于点C,连结OC并延长交EA于点P.
