题目内容
5.根据以下提供的n边形信息,求n边形的内角和.(1)n边形的对角线总条数为$\frac{n(n-3)}{2}$(n≥3)
(2)n边形的对角线总条数与边数相等.
分析 根据n边形的对角线总条数与边数相等,可得多边形,再根据多边形的内角和公式,可得答案.
解答 解:由题意,得
$\frac{n(n-3)}{2}$=n,即n2-5n=0,
解得n=5,n=0舍,
由内角和公式,得
(n-2)•180°=(5-2)×180°=540°.
点评 本题考查了多边形的内角与外角,利用n边形的对角线总条数与边数相等得出方程是解题关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
13.某共享单车前a公里1元,超过a公里的,每公里2元,若要使使用该共享单车50%的人只花1元钱,a应该要取什么数( )
| A. | 平均数 | B. | 中位数 | C. | 众数 | D. | 方差 |
17.为选拔一名选手参加全国中学生游泳锦标赛自由泳比赛,我市四名中学生参加了男子100米自由泳训练,他们成绩的平均数$\overline{x}$及其方差s2如下表所示:
如果选拔一名学生去参赛,应派乙去.
| 甲 | 乙 | 丙 | 丁 | |
| $\overline{x}$ | 1′05″33 | 1′04″26 | 1′04″26 | 1′07″29 |
| S2 | 1.1 | 1.1 | 1.3 | 1.6 |
15.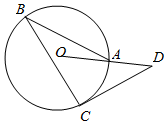 如图,点A,B,C在⊙O上,∠ABC=29°,过点C作⊙O的切线交OA的延长线于点D,则∠D的大小为( )
如图,点A,B,C在⊙O上,∠ABC=29°,过点C作⊙O的切线交OA的延长线于点D,则∠D的大小为( )
 如图,点A,B,C在⊙O上,∠ABC=29°,过点C作⊙O的切线交OA的延长线于点D,则∠D的大小为( )
如图,点A,B,C在⊙O上,∠ABC=29°,过点C作⊙O的切线交OA的延长线于点D,则∠D的大小为( )| A. | 29° | B. | 32° | C. | 42° | D. | 58° |
 如图,在菱形ABCD中,AB=5,对角线BD=6,DF⊥AB于点F.求DF的长.
如图,在菱形ABCD中,AB=5,对角线BD=6,DF⊥AB于点F.求DF的长.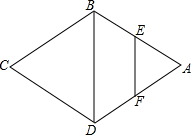 如图,在菱形ABCD中,∠A=60°,E、F分别是AB、AD的中点,若EF=2,求菱形的周长.
如图,在菱形ABCD中,∠A=60°,E、F分别是AB、AD的中点,若EF=2,求菱形的周长.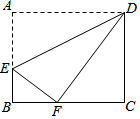 如图,矩形ABCD中,点E在边AB上,将一边AD折叠,使点A恰好落在边BC的点F处,折痕为DE,若AB=8,BF=4,则BC=10cm.
如图,矩形ABCD中,点E在边AB上,将一边AD折叠,使点A恰好落在边BC的点F处,折痕为DE,若AB=8,BF=4,则BC=10cm.