题目内容
16. 自主学习,请阅读下列解题过程.
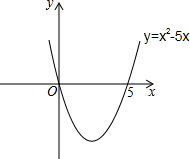
自主学习,请阅读下列解题过程.解一元二次不等式:x2-5x>0
解:设x2-5x=0,解得x1=0,x2=5,则抛物线y=x2-5x与x轴的交点坐标为(0,0)和(5,0).画出二次函数y=x2-5x的大致图象(如图所示),由图象可知:当x<0,或x>5时函数图象位于x轴上方,此时y>0,即x2-5x>0,所以,一元二次不等式x2-5x>0的解集为:x<0,或x>5.
通过对上述解题过程的学习,按其解题的思路和方法解答下列问题:
(1)一元二次不等式x2-5x<0的解集为0<x<5.
(2)用类似的方法解一元二次不等式:x2-2x-3>0.
分析 (1)观察图象即可写出一元二次不等式:x2-5x<0的解集;
(2)先设函数解析式,根据a的值确定抛物线的开口向上,再找出抛物线与x轴相交的两点,就可以画出抛物线,根据y>0确定一元二次不等式x2-2x-3>0的解集.
解答 解:(1)由例题的图形可得:一元二次不等式x2-5x<0的解集为:0<x<5;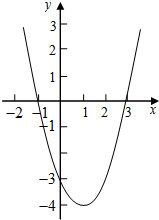
故答案为:0<x<5;
(2)设y=x2-2x-3,则y是x的二次函数.
∵a=1>0,
∴抛物线开口向上.
又∵当y=0时,x2-2x-3=0,
解得:x1=-1,x2=3.
∴由此得抛物线y=x2-2x-3的大致图象如图所示.
观察函数图象可知:当x<-1或x>3时,y>0.
∴x2-2x-3>0的解集是:x<-1或x>3.
点评 本题主要考查了二次函数与不等式以及在直角坐标系中利用二次函数图象解不等式,利用作图结合交点直观求解集是解题关键.

练习册系列答案
相关题目
4.$\frac{2}{3}$sin60°的值等于( )
| A. | $\frac{1}{3}$ | B. | $\frac{\sqrt{3}}{6}$ | C. | $\frac{\sqrt{3}}{3}$ | D. | $\frac{4}{3}$$\sqrt{3}$ |
8.在学校组织的科学素养竞赛中,每班参加比赛的人数相同,成绩分为A,B,C,D四个等级,其中相应等级的得分依次记为90分,80分,70分,60分,学校将八年级一班和二班的成绩整理并绘制成如下的统计图:
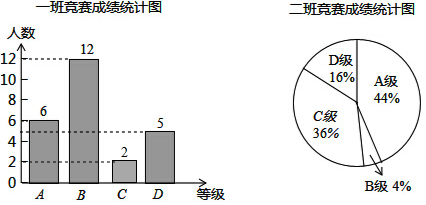
请你根据以上提供的信息解答下列问题:
(1)此次竞赛中二班成绩在70分及其以上的人数有21人;
(2)补全下表中空缺的三个统计量:
(3)请根据上述图表对这次竞赛成绩进行分析,写出两个结论.

请你根据以上提供的信息解答下列问题:
(1)此次竞赛中二班成绩在70分及其以上的人数有21人;
(2)补全下表中空缺的三个统计量:
| 平均数(分) | 中位数(分) | 众数(分) | |
| 一班 | 77.6 | 80 | 80 |
| 二班 | 77.6 | 70 | 90 |
 将下列各选项中的平面图形绕轴旋转一周,可得到图中所示的立体图形的是( )
将下列各选项中的平面图形绕轴旋转一周,可得到图中所示的立体图形的是( )



 如图,已知A(1,6)B(n,-2)是一次函数y=kx+b的图象和反比例函数y=$\frac{m}{x}$的图象的两个交点,直线与y轴交于C点.
如图,已知A(1,6)B(n,-2)是一次函数y=kx+b的图象和反比例函数y=$\frac{m}{x}$的图象的两个交点,直线与y轴交于C点.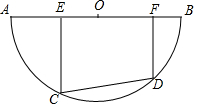 如图,半圆O的直径AB=10,有一条定长为6的动弦CD在弧AB上滑动(点C、点D分别不与点A、点B重合),点E、F在AB上,EC⊥CD,FD⊥CD.
如图,半圆O的直径AB=10,有一条定长为6的动弦CD在弧AB上滑动(点C、点D分别不与点A、点B重合),点E、F在AB上,EC⊥CD,FD⊥CD.