��Ŀ����
ij��ˮ��Ŀ���ˮ��Ϊ12000��m3�������꽵ˮ�����䣬��ά�ָ���16����20�����ˮ����Ϊʵʩ�����裬��Ǩ����4���˺�ˮ��ֻ�ܹ�ά�־���15�����ˮ����
��1���ʣ��꽵ˮ��Ϊ������m3��ÿ����ƽ����ˮ������m3��
��2���������ٽ�Լ��ˮ��ϣ����ˮ���ʹ��������ߵ�25�꣮���������˾�ÿ�����Լ����m3ˮ����ʵ��Ŀ�ꣿ
��3��ij��ҵͶ��1000��Ԫ�豸��ÿ���ܵ���5000m3��ˮ��������Ϊ70%��ÿ����1m3��ˮ����ķ���Ϊ1.5Ԫ����������0.3Ԫ����ҵ������ˮ��3.2Ԫ/m3�ļ۸���ۣ�ÿ�껹�����֧��40��Ԫ����ÿ��ʵ������300����㣬����ҵ���ټ�������ջسɱ��������ȷ����λ����
 ��������
��1�����꽵ˮ��Ϊx��m3��ÿ����ƽ����ˮ��Ϊym3��
������������
���꽵ˮ��Ϊ200��m3��ÿ����ƽ����ˮ��Ϊ50m3��
��2�����������˾�ÿ�����Լz m3ˮ����ʵ��Ŀ�꣬
������ã�12000+25��200=20��25z����ã�z=34��
50��34=16m3��
�����������˾�ÿ�����Լ16 m3ˮ����ʵ��Ŀ�ꡣ
��3��...
��������
��1�����꽵ˮ��Ϊx��m3��ÿ����ƽ����ˮ��Ϊym3��
������������
���꽵ˮ��Ϊ200��m3��ÿ����ƽ����ˮ��Ϊ50m3��
��2�����������˾�ÿ�����Լz m3ˮ����ʵ��Ŀ�꣬
������ã�12000+25��200=20��25z����ã�z=34��
50��34=16m3��
�����������˾�ÿ�����Լ16 m3ˮ����ʵ��Ŀ�ꡣ
��3��...
����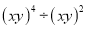 �Ľ���ǣ� ��
�Ľ���ǣ� ��
A. 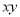 B.
B. 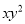 C.
C. 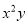 D.
D. 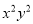
 D
����������������� ���ʴ���Dѡ��.
��ѡD.
D
����������������� ���ʴ���Dѡ��.
��ѡD. ����•�ġ�����ڣ�����ί��֯������ѧ����Աȥ��ɽֲ����ijУ���꼶��3������֧���쵽һ�����磬��ÿ��ֲ4��������ʣ37�ã���ÿ��ֲ6�����������һ������ֲ��������3�ã��������繲��__�ã�
 121
����������������
������ί��֯������ѧ����Ա��x�ˣ��������У�4x+37���ã�������ã�
1�ܣ�4x+37����6��x��1����3
ȥ���ŵã�1�ܩ�2x+43��3��
����ã���42�ܩ�2x����40��
��ã�20��x��21��
��xȡ����������x=21��
��x=21ʱ��4x+37=4��21+37=121����������4��21+37=121�ã�
�ʴ�...
121
����������������
������ί��֯������ѧ����Ա��x�ˣ��������У�4x+37���ã�������ã�
1�ܣ�4x+37����6��x��1����3
ȥ���ŵã�1�ܩ�2x+43��3��
����ã���42�ܩ�2x����40��
��ã�20��x��21��
��xȡ����������x=21��
��x=21ʱ��4x+37=4��21+37=121����������4��21+37=121�ã�
�ʴ�... ���в���ʽ�У���һԪһ�β���ʽ����( )
A. 2x-1��0 B. -1��2 C. 3x-2y��-1 D. y2+3��5
 A
��������A����һԪһ�β���ʽ��
B������δ֪���������϶��壻
C����������δ֪���������϶��壻
D��δ֪���Ĵ�����2�������϶��壻
��ѡA��
A
��������A����һԪһ�β���ʽ��
B������δ֪���������϶��壻
C����������δ֪���������϶��壻
D��δ֪���Ĵ�����2�������϶��壻
��ѡA�� ��ͼ�����������ܱ�֤��ABC�ա�ADC���ǣ���AB=AD��BC=DC���ڡ�1=��3����4=��2���ۡ�1=��2����4=��3���ܡ�1=��2��AB=AD���ݡ�1=��2��BC=DC����������
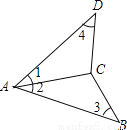
A. �٢ڢۢܢ� B. �٢ڢۢ� C. �٢ۢ� D. �٢ۢܢ�
 C
�����������ڡ�ABC�͡�ADC�У�AC=AC��
�൱������������AB=AD��BC=DCʱ�����ɡ�SSS���õ���ABC�ա�ADC��
�������������ڡ�1=��3����4=��2ʱ�����ܵõ���ABC�ա�ADC��
�������������ۡ�1=��2����4=��3ʱ�����ɡ�AAS���õ���ABC�ա�ADC��
�������������ܡ�1=��2��AB=ADʱ�����ɡ�SAS���õ���ABC�ա�ADC��
...
C
�����������ڡ�ABC�͡�ADC�У�AC=AC��
�൱������������AB=AD��BC=DCʱ�����ɡ�SSS���õ���ABC�ա�ADC��
�������������ڡ�1=��3����4=��2ʱ�����ܵõ���ABC�ա�ADC��
�������������ۡ�1=��2����4=��3ʱ�����ɡ�AAS���õ���ABC�ա�ADC��
�������������ܡ�1=��2��AB=ADʱ�����ɡ�SAS���õ���ABC�ա�ADC��
... ij�̳��Ƴ�һ�ֹ������ƾ���ڸ��̳�����ɰ���Ʒ�۸�İ����Żݣ���������ʱÿ��Ҫ��100Ԫ�����ѣ��谴����ۼƹ�����Ϊx��Ԫ������x��__ʱ����������ʡǮ��
 500
����������������
������ã�x��0.8x��100����ã�x��500��
�������������500Ԫʱ����������ʡǮ��
�ʴ�Ϊ��500��
500
����������������
������ã�x��0.8x��100����ã�x��500��
�������������500Ԫʱ����������ʡǮ��
�ʴ�Ϊ��500�� С������1.5�ף�С���ְ�����1.8�ף�С������һ��ÿ����a�ף���10����ƽ̨˵�����ְ֣���������������߶��Ȳ������ˣ����ɴ˿ɵù���a�IJ���ʽ�ǣ�������
A. 10a��1.8��2 B. 1.5+a+10��1.8��2 C. 10a+1.5��1.8��2 D. 1.8��2��10a+15
 C
������������С��������+10����̨�ĸ߶ȣ��ְ����ߵ�2����ʽ���ɣ�
��������
�������⣬��10a+1.5��1.8��2��
��ѡ��C��
C
������������С��������+10����̨�ĸ߶ȣ��ְ����ߵ�2����ʽ���ɣ�
��������
�������⣬��10a+1.5��1.8��2��
��ѡ��C�� ����ʽ��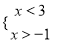 �Ľ⼯��_________��
�Ľ⼯��_________��
 ��1��x��3
�����������ݡ�С���С�м��ҡ���ԭ���������ʽ��Ľ⼯���ɣ�
�ߩ�1��3��
��˲���ʽ��Ľ⼯Ϊ����1��x��3��
�ʴ�Ϊ����1��x��3��
��1��x��3
�����������ݡ�С���С�м��ҡ���ԭ���������ʽ��Ľ⼯���ɣ�
�ߩ�1��3��
��˲���ʽ��Ľ⼯Ϊ����1��x��3��
�ʴ�Ϊ����1��x��3�� ��ͼ����ABCD�У�BD������һ���Խ��ߣ���A��C������AE��BD��CF��BD������ֱ�ΪE��F���ӳ�AE��CF�ֱ�CD��AB��M��N��
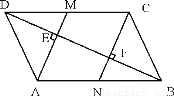
��1����֤���ı���CMAN��ƽ���ı��Ρ�
��2����֪DE��4��FN��3����BN�ij���
 ��1�������������2��5��
��������
�����������1��ͨ��AE��BD��CF��BD֤��AE��CF�������ı���ABCD��ƽ���ı��εõ�AB��CD��������Ա߷ֱ�ƽ�е��ı�����ƽ���ı��ο�֤���ı���CMAN��ƽ���ı��Σ���2��֤����MDE�ա�NBF������ȫ�������ε����ʿɵ�DE=BF=4�����ɹ��ɶ�����BN=5��
�����������1��֤������AE��BD CF��BD
��AE��CF
...
��1�������������2��5��
��������
�����������1��ͨ��AE��BD��CF��BD֤��AE��CF�������ı���ABCD��ƽ���ı��εõ�AB��CD��������Ա߷ֱ�ƽ�е��ı�����ƽ���ı��ο�֤���ı���CMAN��ƽ���ı��Σ���2��֤����MDE�ա�NBF������ȫ�������ε����ʿɵ�DE=BF=4�����ɹ��ɶ�����BN=5��
�����������1��֤������AE��BD CF��BD
��AE��CF
... 
