题目内容
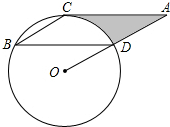 如图,点B、C、D都在⊙O上,过C点作CA∥BD交OD的延长线于点A,连接BC,∠B=∠A=30°,BD=2
如图,点B、C、D都在⊙O上,过C点作CA∥BD交OD的延长线于点A,连接BC,∠B=∠A=30°,BD=2| 3 |
(1)求证:AC是⊙O的切线;
(2)求由线段AC、AD与弧CD所围成的阴影部分的面积.(结果保留π)
考点:切线的判定,扇形面积的计算
专题:几何综合题
分析:(1)连接OC,根据圆周角定理求出∠COA,根据三角形内角和定理求出∠OCA,根据切线的判定推出即可;
(2)求出DE,解直角三角形求出OC,分别求出△ACO的面积和扇形COD的面积,即可得出答案.
(2)求出DE,解直角三角形求出OC,分别求出△ACO的面积和扇形COD的面积,即可得出答案.
解答: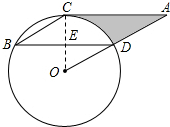 (1)证明:连接OC,交BD于E,
(1)证明:连接OC,交BD于E,
∵∠B=30°,∠B=
∠COD,
∴∠COD=60°,
∵∠A=30°,
∴∠OCA=90°,
即OC⊥AC,
∴AC是⊙O的切线;
(2)解:∵AC∥BD,∠OCA=90°,
∴∠OED=∠OCA=90°,
∴DE=
BD=
,
∵sin∠COD=
,
∴OD=2,
在Rt△ACO中,tan∠COA=
,
∴AC=2
,
∴S阴影=
×2×2
-
=2
-
.
 (1)证明:连接OC,交BD于E,
(1)证明:连接OC,交BD于E,∵∠B=30°,∠B=
| 1 |
| 2 |
∴∠COD=60°,
∵∠A=30°,
∴∠OCA=90°,
即OC⊥AC,
∴AC是⊙O的切线;
(2)解:∵AC∥BD,∠OCA=90°,
∴∠OED=∠OCA=90°,
∴DE=
| 1 |
| 2 |
| 3 |
∵sin∠COD=
| DE |
| OD |
∴OD=2,
在Rt△ACO中,tan∠COA=
| AC |
| OC |
∴AC=2
| 3 |
∴S阴影=
| 1 |
| 2 |
| 3 |
| 60π×22 |
| 360 |
| 3 |
| 2π |
| 3 |
点评:本题考查了平行线的性质,圆周角定理,扇形的面积,三角形的面积,解直角三角形等知识点的综合运用,题目比较好,难度适中.

练习册系列答案
相关题目
已知a、b、c是有理数,下列不等式变形中,一定正确的是( )
| A、若ac>bc,则a>b |
| B、若a>b,则ac>bc |
| C、若ac2>bc2,则a>b |
| D、若a>b,则ac2>bc2 |
某同学随机将一枚硬币抛向空中20次,有12次出现反面,那么正面出现的频率是( )
| A、0.12 | B、0.4 |
| C、0.8 | D、0.6 |
 已知:如图,D、E、F分别是BC、CA、AB上的点,DE∥AB,DF∥CA.求证:∠EDF=∠A(写出证明过程,并注明各步理由)
已知:如图,D、E、F分别是BC、CA、AB上的点,DE∥AB,DF∥CA.求证:∠EDF=∠A(写出证明过程,并注明各步理由) 在平行四边形ABCD中,将△ABC沿AC对折,使点B落在B′处,A B′和CD相交于点O.求证:OA=OC.
在平行四边形ABCD中,将△ABC沿AC对折,使点B落在B′处,A B′和CD相交于点O.求证:OA=OC.