题目内容
 在平行四边形ABCD中,将△ABC沿AC对折,使点B落在B′处,A B′和CD相交于点O.求证:OA=OC.
在平行四边形ABCD中,将△ABC沿AC对折,使点B落在B′处,A B′和CD相交于点O.求证:OA=OC.考点:平行四边形的性质,等腰三角形的判定与性质,翻折变换(折叠问题)
专题:证明题
分析:由在平行四边形ABCD中,将△ABC沿AC对折,使点B落在B′处,即可求得∠DCA=∠B′AC,则可证得OA=OC.
解答:证明:∵△AB′C是由△ABC沿AC对折得到的图形,
∴∠BAC=∠B′AC,
∵在平行四边形ABCD中,AB∥CD,
∴∠BAC=∠DCA,
∴∠DCA=∠B′AC,
∴OA=OC.
∴∠BAC=∠B′AC,
∵在平行四边形ABCD中,AB∥CD,
∴∠BAC=∠DCA,
∴∠DCA=∠B′AC,
∴OA=OC.
点评:此题考查了平行四边形的性质、等腰三角形的判定与性质以及折叠的性质.此题难度不大,注意掌握折叠前后图形的对应关系,注意掌握数形结合思想的应用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知直线y=-
x+3分别与x轴,y轴交于A,B两点,O为坐标原点,则△AOB的面积是( )
| 1 |
| 2 |
| A、6 | B、9 | C、15 | D、18 |
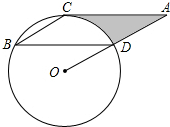 如图,点B、C、D都在⊙O上,过C点作CA∥BD交OD的延长线于点A,连接BC,∠B=∠A=30°,BD=2
如图,点B、C、D都在⊙O上,过C点作CA∥BD交OD的延长线于点A,连接BC,∠B=∠A=30°,BD=2
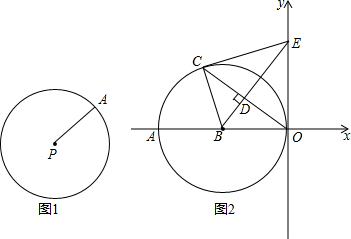
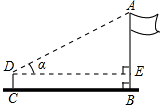 某校九年级四个数学活动小组参加测量操场旗杆高度的综合实践活动,如图是四个小组在不同位置测量后绘制的示意图,用测角仪测得旗杆顶端A的仰角记为α,CD为测角仪的高,测角仪CD的底部C处与旗杆的底部B处之间的距离记为CB,四个小组测量和计算数据如下表所示:
某校九年级四个数学活动小组参加测量操场旗杆高度的综合实践活动,如图是四个小组在不同位置测量后绘制的示意图,用测角仪测得旗杆顶端A的仰角记为α,CD为测角仪的高,测角仪CD的底部C处与旗杆的底部B处之间的距离记为CB,四个小组测量和计算数据如下表所示: