题目内容
已知点A1(a1,a2),A2(a2,a3),A3(a3,a4)…,An(an,an+1)(n为正整数)都在一次函数y=x+3的图象上.若a1=2,则a2014= .
考点:一次函数图象上点的坐标特征
专题:规律型
分析:将a1=2代入a2=x+3,依次求出a1、a2、a3、a4、a5、a6…的值,找到规律然后解答.
解答:解:将a1=2代入a2=x+3,得a2=5,
同理可求得,a3=8,a4=11,a5=14,a6=17,
an=2+3(n-1),
a2014=2+3(2014-1)=2+3×2013=2+6039=6041,
故答案为:6041.
同理可求得,a3=8,a4=11,a5=14,a6=17,
an=2+3(n-1),
a2014=2+3(2014-1)=2+3×2013=2+6039=6041,
故答案为:6041.
点评:本题考查了一次函数图象上点的坐标特征,计算出结果,找到规律即可解答.

练习册系列答案
 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案
相关题目
已知直线y=-
x+3分别与x轴,y轴交于A,B两点,O为坐标原点,则△AOB的面积是( )
| 1 |
| 2 |
| A、6 | B、9 | C、15 | D、18 |
 如图,已知∠DAB=70°,AC平分∠DAB,∠1=35°,求∠D的度数.
如图,已知∠DAB=70°,AC平分∠DAB,∠1=35°,求∠D的度数. 如图,∠A=15°,AB=BC=CD=DE=EF,则∠GEF=
如图,∠A=15°,AB=BC=CD=DE=EF,则∠GEF= 如图,小明爬一土坡,他从A处爬到B处所走的直线距离AB=4米,此时,他离地面高度为h=2米,则这个土坡的坡角为
如图,小明爬一土坡,他从A处爬到B处所走的直线距离AB=4米,此时,他离地面高度为h=2米,则这个土坡的坡角为 如图,直线a、b相交于点O,∠1=50°,则∠2=
如图,直线a、b相交于点O,∠1=50°,则∠2=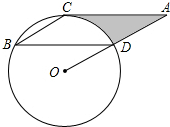 如图,点B、C、D都在⊙O上,过C点作CA∥BD交OD的延长线于点A,连接BC,∠B=∠A=30°,BD=2
如图,点B、C、D都在⊙O上,过C点作CA∥BD交OD的延长线于点A,连接BC,∠B=∠A=30°,BD=2