题目内容
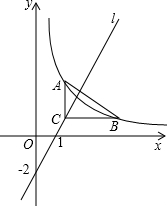 已知直线l经过点(1,0)(0,-2),Rt△ABC如图放置,其直角顶点C在直线l上,两直角边分别平行于坐标轴,AC=2,BC=3,将Rt△ABC沿直线l平移,使点A、B都在函数y=
已知直线l经过点(1,0)(0,-2),Rt△ABC如图放置,其直角顶点C在直线l上,两直角边分别平行于坐标轴,AC=2,BC=3,将Rt△ABC沿直线l平移,使点A、B都在函数y=| k |
| x |
考点:反比例函数图象上点的坐标特征,坐标与图形变化-平移
专题:
分析:过点B作BM⊥x轴于点M,过点A作AN⊥y轴于点N,延长AC交x轴于点D,设点C的坐标为(m,2m-2),根据反比例函数上的点向x轴y轴引垂线形成的矩形面积等于反比例函数的k值是个定值作为相等关系求得m值后再求算k值.
解答: 解:过点B作BM⊥x轴于点M,过点A作AN⊥y轴于点N,延长AC交x轴于点D,
解:过点B作BM⊥x轴于点M,过点A作AN⊥y轴于点N,延长AC交x轴于点D,
∵直线l经过点(1,0)(0,-2),
∴直线l解析式为y=2x-2,
设点C的坐标为(m,2m-2),则
∵AC=2,BC=3
∴OM=3+m,ON=2m-2+2=2m,
∴B(3+m,2m-2),A(m,2m),
∴m•2m=(3+m)(2m-2)=k,
解得,m=
,
∴k=m•2m=
.
故答案为
.
 解:过点B作BM⊥x轴于点M,过点A作AN⊥y轴于点N,延长AC交x轴于点D,
解:过点B作BM⊥x轴于点M,过点A作AN⊥y轴于点N,延长AC交x轴于点D,∵直线l经过点(1,0)(0,-2),
∴直线l解析式为y=2x-2,
设点C的坐标为(m,2m-2),则
∵AC=2,BC=3
∴OM=3+m,ON=2m-2+2=2m,
∴B(3+m,2m-2),A(m,2m),
∴m•2m=(3+m)(2m-2)=k,
解得,m=
| 3 |
| 2 |
∴k=m•2m=
| 9 |
| 2 |
故答案为
| 9 |
| 2 |
点评:此题综合考查了反比例函数与一次函数的性质,此题难度稍大,综合性比较强,注意反比例函数上的点向x轴y轴引垂线形成的矩形面积等于反比例函数的k值.

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目
 如图,在10×6的方格纸中有两个格点△ABC和△DEF,若△DEF是由△ABC平移得到的,则下列平移法正确的是( )
如图,在10×6的方格纸中有两个格点△ABC和△DEF,若△DEF是由△ABC平移得到的,则下列平移法正确的是( )| A、把△ABC先向左平移4个单位,再向下平移2个单位 |
| B、把△ABC先向右平移4个单位,再向下平移2个单位 |
| C、把△ABC先向右平移4个单位,再向上平移2个单位 |
| D、把△ABC先向左平移4个单位,再向上平移2个单位 |
 如图,不能判定EB∥AC的条件是( )
如图,不能判定EB∥AC的条件是( )| A、∠C=∠DBE |
| B、∠A=∠ABE |
| C、∠C+∠EBC=180° |
| D、∠C=∠ABC |
 如图,AB∥CD,直线EF与AB,CD分别交于点G,H,GM平分∠BGH交CD于点M,∠1=50°,则∠2=
如图,AB∥CD,直线EF与AB,CD分别交于点G,H,GM平分∠BGH交CD于点M,∠1=50°,则∠2=