题目内容
20．
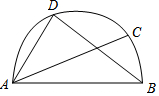如图，AB是半圆的直径，∠BAC=20°，D是$\widehat{AC}$的中点，则∠DAC的度数是（ ）| A． | 30° | B． | 35° | C． | 45° | D． | 70° |
分析 首先连接BC，由AB是半圆的直径，根据直径所对的圆周角是直角，可得∠C=90°，继而求得∠ABC的度数，然后由D是$\widehat{AC}$的中点，根据弧与圆周角的关系，即可求得答案．
解答 解：连接BC，
∵AB是半圆的直径，
∴∠C=90°，
∵∠BAC=20°，
∴∠B=90°-∠BAC=70°，
∵D是$\widehat{AC}$的中点，
∴∠DAC=$\frac{1}{2}$∠ABC=35°．
故选：B．
点评 此题考查了圆周角定理．注意准确作出辅助线是解此题的关键．
练习册系列答案
相关题目
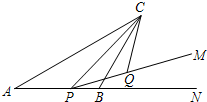如图，△ABC中，AC=10，∠BAC=30°，点P是射线AB上的一个动点，∠CPM=30°，点Q是射线PM上的一个动点．则CQ长度的最小值是$\frac{5}{2}$．
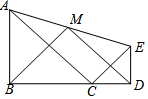如图，△ABC和△CDE均为等腰直角三角形，点B、C、D在一条直线上，点M是AE的中点，