题目内容
 已知直角三角形ABC的内切圆与三条边分别切于点D、E、F,若AC=3cm,BC=4cm,求内切圆半径的大小.
已知直角三角形ABC的内切圆与三条边分别切于点D、E、F,若AC=3cm,BC=4cm,求内切圆半径的大小.考点:三角形的内切圆与内心
专题:
分析:首先利用勾股定理求出AB的长,再利用三角形面积得出内切圆半径.
解答:解:∵∠C=90°,AC=3cm,BC=4cm,
∴AB=
=5(cm),
故
×3×4=
r(AC+BC+AB)=
r×12,
解得:r=1.
∴AB=
| 42+32 |
故
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解得:r=1.
点评:此题主要考查了三角形内心以及三角形面积,表示出△ACB面积是解题关键.

练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案
相关题目
⊙O的半径为4,直线l与⊙O相切,则O到直线l的距离是( )
| A、小于4 | B、等于4 |
| C、大于4 | D、无法确定 |
 如图,等边△ABC内接于⊙O,P是
如图,等边△ABC内接于⊙O,P是
 如图,∠AOC=∠BOD=90°,OE是∠AOB的平分线,且∠COE=75°,
如图,∠AOC=∠BOD=90°,OE是∠AOB的平分线,且∠COE=75°,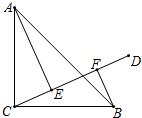 如图,在△ABC中,∠ABC=90°,AC=BC,AE⊥CD,BF⊥CD,垂足分别为点E,F,图中BF与哪条线段相等?说明理由.
如图,在△ABC中,∠ABC=90°,AC=BC,AE⊥CD,BF⊥CD,垂足分别为点E,F,图中BF与哪条线段相等?说明理由. 已知如图,△ABC是等腰直角三角形,∠BAC=90°,将△ABP绕点A逆时针方向转动到△ACP′,若AP=3cm,AB=4cm,求BC、PP′的长.
已知如图,△ABC是等腰直角三角形,∠BAC=90°,将△ABP绕点A逆时针方向转动到△ACP′,若AP=3cm,AB=4cm,求BC、PP′的长. 如图,AB是半⊙的直径,AC为弦,D为
如图,AB是半⊙的直径,AC为弦,D为