题目内容
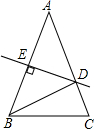 如图,△ABC是等腰三角形,且顶角∠A=36°,DE是AB的垂直平分线,则有:
如图,△ABC是等腰三角形,且顶角∠A=36°,DE是AB的垂直平分线,则有:①BD平分∠ABC;②AD=BD=BC;③AD=CD;④△BCD的周长=AB+BC,
其中正确的有( )个.
| A、1个 | B、2个 | C、3个 | D、4个 |
考点:等腰三角形的判定与性质,线段垂直平分线的性质
专题:
分析:根据线段垂直平分线的性质,可判断①,根据等角对等边,可判断②,根据线段垂直平分线BD+DC与AC的关系,再根据等量代换,可得④的答案.
解答:解:△ABC是等腰三角形,且顶角∠A=36°,
∴∠ABC=∠ACB=72°,
∵DE是AB的垂直平分线,
∴AD=BD,
∠ABD=∠A=∠DBC=36°,故①正确;
∵∠DBC=36°,∠DCB=72°,
∴∠BCD=∠DCB=72°,
∴AD=DB=BC,故②正确;
∵∠DBC=36°≠∠DCB
∴BD≠CD,
∴AD≠CD故③错误;
∴AD=BD,
∴BD+DC+BC=AC+BC,
∴④△BCD的周长=AB+BC,故④正确;
故选:C.
∴∠ABC=∠ACB=72°,
∵DE是AB的垂直平分线,
∴AD=BD,
∠ABD=∠A=∠DBC=36°,故①正确;
∵∠DBC=36°,∠DCB=72°,
∴∠BCD=∠DCB=72°,
∴AD=DB=BC,故②正确;
∵∠DBC=36°≠∠DCB
∴BD≠CD,
∴AD≠CD故③错误;
∴AD=BD,
∴BD+DC+BC=AC+BC,
∴④△BCD的周长=AB+BC,故④正确;
故选:C.
点评:本题考查了等腰三角形的判定与性质,等腰三角形的两底角相等,两个角相等的三角形是等腰三角形.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,若数轴上的点A,B,C,D表示数-2,1,2,3,则表示4-
如图,若数轴上的点A,B,C,D表示数-2,1,2,3,则表示4-| 3 |
| A、线段AB上 |
| B、线段BC上 |
| C、线段CD上 |
| D、线段OB上 |
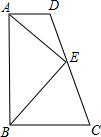 如图,四边形ABCD中,AD∥BC,点E是CD的中点,连接AE、BE,∠EAD=∠EAB.给出下列五个结论:
如图,四边形ABCD中,AD∥BC,点E是CD的中点,连接AE、BE,∠EAD=∠EAB.给出下列五个结论:①BE⊥AE;②BE平分∠ABC;③AD+BC=AB;④AB⊥BC;⑤△ABC=
| 1 |
| 2 |
其中正确的有( )
| A、2 | B、3 | C、4 | D、5 |
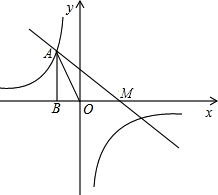 如图,已知反比例函数y=
如图,已知反比例函数y=