题目内容
已知一个三角形中相邻两边的长分别是6cm和4cm，第三边上的高是2cm，试求出第三边的长为多少？
考点：勾股定理
专题：分类讨论
分析：根据题意画出图形，再根据勾股定理求解即可．
解答：
解：当如图1所示时，△ABC中，AB=6，AC=4，AD⊥BC且AD=2，求BC的长．
∵AB=6，AC=4，AD⊥BC且AD=2，
∴BD=
=
=4
，CD=
=
=2
，
∴BC=BD+CD=（4
+2
）cm．
当如图2所示时，
BC=BD-CD=（4
-2
）cm．
解：当如图1所示时，△ABC中，AB=6，AC=4，AD⊥BC且AD=2，求BC的长．∵AB=6，AC=4，AD⊥BC且AD=2，
∴BD=
| AB2-AD2 |
| 62-22 |
| 2 |
| AC2-AD2 |
| 42-22 |
| 3 |
∴BC=BD+CD=（4
| 2 |
| 3 |
当如图2所示时，
BC=BD-CD=（4
| 2 |
| 3 |
点评：本题考查的是勾股定理，熟知在任何一个直角三角形中，两条直角边长的平方之和一定等于斜边长的平方是解答此题的关键．
练习册系列答案
阅读快车系列答案
相关题目
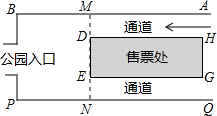如图，公园入口处前有一间售票处，其屋面DEGH是矩形．售票处后墙DE与两侧通道垂直．小亮的爸爸已购公园门票，在点P处等候小亮，小亮沿售票处北侧的通道中央行进，去找爸爸．
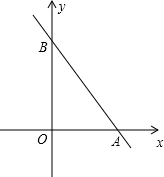直线y=-