题目内容
已知实数x,y满足(2x+1)2+y2+(y-2x)2=
,求x+y的值.
| 1 |
| 3 |
考点:根的判别式
专题:
分析:利用配方法把已知方程转化为两平方数的和的形式,然后由非负数的性质求得x、y的值.从而求得x+y的值.
解答:解:由(2x+1)2+y2+(y-2x)2=
,得
(3x+1)2+3(x-y)2=0,
则
,
解得
,
故x+y=-
-
=-
.
| 1 |
| 3 |
(3x+1)2+3(x-y)2=0,
则
|
解得
|
故x+y=-
| 1 |
| 3 |
| 1 |
| 3 |
| 2 |
| 3 |
点评:本题考查了配方法的应用.此题根据非负数的性质求得x、y的值是解题的难点.

练习册系列答案
相关题目
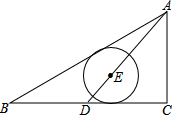 如图,Rt△ABC中,∠C=90°,AB=5,AC=3,D点从BC的中点到C点运动,点E在AD上,以E为圆心的⊙E分别与AB、BC相切,则⊙E的半径R的取值范围为( )
如图,Rt△ABC中,∠C=90°,AB=5,AC=3,D点从BC的中点到C点运动,点E在AD上,以E为圆心的⊙E分别与AB、BC相切,则⊙E的半径R的取值范围为( )A、
| ||||
B、
| ||||
C、
| ||||
D、1≤R≤
|
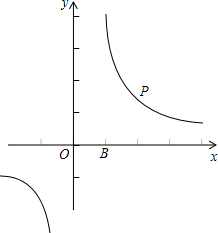 如图,点P是函数y=
如图,点P是函数y= 已知AD⊥BC于点D,D为BC的中点,连接AB,∠ABC的平分线交AD于点O,连接OC,若∠ABO=32°,则∠AOC=
已知AD⊥BC于点D,D为BC的中点,连接AB,∠ABC的平分线交AD于点O,连接OC,若∠ABO=32°,则∠AOC= 如图,甲从A点出发向北偏东70°方向走50m至点B,乙从A出发向南偏西15°方向走30m至点C,则∠BAC的度数是
如图,甲从A点出发向北偏东70°方向走50m至点B,乙从A出发向南偏西15°方向走30m至点C,则∠BAC的度数是