题目内容
1．已知A（-2，5）、B（1，2）、C（2，3）三点的坐标，求：（1）画图并判断△ABC的形状；
（2）证明你的结论．
分析 （1）根据坐标的意义描点即可得到△ABC；
（2）利用两点间的距离公式计算出BC、BA和AC，然后根据勾股定理的逆定理可证明△ABC为直角三角形．
解答 解：（1）如图，△ABC为所作，△ABC为直角三角形；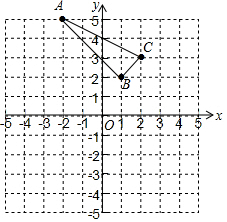
（2）∵BC2=（1-2）2+（2-3）2=2，BA2=（1+2）2+（2-5）2=18，AC2=（-2-2）2+（5-3）2=20，
而2+18=20，
∴BC2+BA2=AC2，
∴△ABC为直角三角形，∠ABC=90°．
点评 本题考查了作图-复杂作图：复杂作图是在五种基本作图的基础上进行作图，一般是结合了几何图形的性质和基本作图方法．解决此类题目的关键是熟悉基本几何图形的性质，结合几何图形的基本性质把复杂作图拆解成基本作图，逐步操作．也考查了两点间的距离公式和勾股定理的逆定理．
练习册系列答案
相关题目
11．摩托车厂本周计划每天生产250辆摩托车，由于工人实行轮休，每天上班的人数不一定相等，实际每天生产量（与计划量相比）的增长值如表：
根据上面的记录，问：哪几天生产的摩托车比计划量多？星期几生产的摩托车最多，是多少辆？星期几生产的摩托车最少，是多少辆？
| 星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
| 增减 | -5 | +7 | -3 | +4 | +10 | -9 | -25 |
如图所示，正方形OABC的两边OA，OC分别在x轴、y轴上，点D（5，3）在边AB上，以点C为中心，把△CDB旋转90°．
如图，在四边形ABCD中，AB∥CD，AD∥BC，AB=CD，AD=BC，点E是AD的中点，连接BE并延长交CD的延长线于点F．