题目内容
5.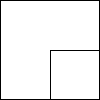 如图是一幅“斜阳正方形”,最大正方形的边长为a米,第二个正方形的边长是$\frac{a}{2}$米,第三个正方形的边长是$\frac{a}{4}$米,…以此类推.
如图是一幅“斜阳正方形”,最大正方形的边长为a米,第二个正方形的边长是$\frac{a}{2}$米,第三个正方形的边长是$\frac{a}{4}$米,…以此类推.①求第一个正方形到第四个正方形的周长的和与面积的和.
②当a=16米时,求①中的周长的和与面积的和.
分析 ①由题意可知:第一个正方形的边长为a米,第二个正方形的边长是$\frac{a}{2}$米,第三个正方形的边长是$\frac{a}{4}$米,第四个正方形的边长为$\frac{a}{8}$米,利用正方形的周长和面积计算公式列式计算即可;
②把a=16代入①中的代数式求得数值即可.
解答 解:①∵第一个正方形的边长为a米,第二个正方形的边长是$\frac{a}{2}$米,第三个正方形的边长是$\frac{a}{4}$米,第四个正方形的边长为$\frac{a}{8}$米,
∴四个正方形的周长的和=4(a+$\frac{a}{2}$+$\frac{a}{4}$+$\frac{a}{8}$)=$\frac{15}{2}$a米;
面积的和=a2+($\frac{a}{2}$)2+($\frac{a}{4}$)2+($\frac{a}{8}$)2=$\frac{85}{64}$a2平方米;
②当a=16米时,
周长的和=120米;
面积的和=340平方米.
点评 此题考查列代数式,代数式求值,掌握正方形的周长和面积计算公式是解决问题的关键.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
14.观察下列图形中点的个数,根据其中蕴含的规律回答下列问题:
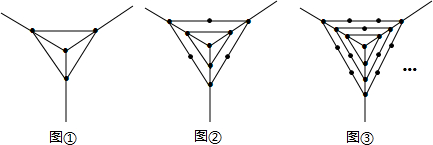
(1)填写下表:
(2)用代数式表示第n个图形中点的个数$\frac{3}{2}$n(n+1)+1个.

(1)填写下表:
| 图形编号 | ① | ② | ③ | … |
| 图形中点的个数 | 4 | 10 | 19 |
 如图,在△ABC中,∠B=2∠C,点D在BC边上,且AD⊥AC,求证:CD=2AB.
如图,在△ABC中,∠B=2∠C,点D在BC边上,且AD⊥AC,求证:CD=2AB. 图中有阴影的三角形与哪些三角形成轴对称?整个图形是轴对称图形吗?它共有几条对称轴?
图中有阴影的三角形与哪些三角形成轴对称?整个图形是轴对称图形吗?它共有几条对称轴? 如图,△AOB∽△COD,∠A=∠C.有下列各式:①$\frac{AB}{BO}$=$\frac{CD}{CO}$;②$\frac{AB}{AO}$=$\frac{CD}{OD}$;③$\frac{OB}{CO}$=$\frac{AD}{OD}$;④$\frac{AO}{OC}$=$\frac{BO}{OD}$.其中正确的有( )
如图,△AOB∽△COD,∠A=∠C.有下列各式:①$\frac{AB}{BO}$=$\frac{CD}{CO}$;②$\frac{AB}{AO}$=$\frac{CD}{OD}$;③$\frac{OB}{CO}$=$\frac{AD}{OD}$;④$\frac{AO}{OC}$=$\frac{BO}{OD}$.其中正确的有( ) 如图所示,在5×5的正方形网格中,有格点△ABC,请你在图中画出符合下列三个要求的最小△A1B1C1和最大△A2B2C2.
如图所示,在5×5的正方形网格中,有格点△ABC,请你在图中画出符合下列三个要求的最小△A1B1C1和最大△A2B2C2.  如图所示,△ABC为等边三角形,DB=DE,∠BDE=120°,F为CE的中点,求证:AF⊥DF.
如图所示,△ABC为等边三角形,DB=DE,∠BDE=120°,F为CE的中点,求证:AF⊥DF.