题目内容
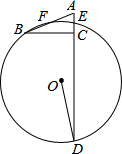
5. 如图,?ABCD的顶点A、B、D在⊙O上,顶点C在⊙O的直径BE上,连接AE交CD于F点,∠E=36°,求∠AFC的度数.
如图,?ABCD的顶点A、B、D在⊙O上,顶点C在⊙O的直径BE上,连接AE交CD于F点,∠E=36°,求∠AFC的度数.
分析 由BE是⊙O的直径,根据直径所对的圆周角是直角,可求得∠BAE=90°,由平行四边形的性质得出AB∥CD,由平行线的性质即可求得答案.
解答 解:如图所示:
∵BE是⊙O的直径,
∴∠BAE=90°,
∵四边形ABCD是平行四边形,
∴AB∥CD,
∴∠BAE+∠AFC=180°,
∴∠AFC=90°.
点评 此题考查了圆周角定理以及平行四边形的性质.根据半圆(或直径)所对的圆周角是直角得出∠BAE=90°是解决问题的突破口.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案
相关题目
10. 如图,△ABC中,AC=5,BC=12,∠ACB=90°,E、F分别为AC、AB中点,过E、F两点作⊙O,延长AC交⊙O于D,若∠CDO=$\frac{1}{2}$∠B,则⊙O的半径为( )
如图,△ABC中,AC=5,BC=12,∠ACB=90°,E、F分别为AC、AB中点,过E、F两点作⊙O,延长AC交⊙O于D,若∠CDO=$\frac{1}{2}$∠B,则⊙O的半径为( )
 如图,△ABC中,AC=5,BC=12,∠ACB=90°,E、F分别为AC、AB中点,过E、F两点作⊙O,延长AC交⊙O于D,若∠CDO=$\frac{1}{2}$∠B,则⊙O的半径为( )
如图,△ABC中,AC=5,BC=12,∠ACB=90°,E、F分别为AC、AB中点,过E、F两点作⊙O,延长AC交⊙O于D,若∠CDO=$\frac{1}{2}$∠B,则⊙O的半径为( )| A. | 13 | B. | $2\sqrt{26}$ | C. | $3\sqrt{26}$ | D. | $\frac{27}{2}$ |
14. 如图,AD⊥BC,ED⊥AB,表示点A到直线DE距离的是( )
如图,AD⊥BC,ED⊥AB,表示点A到直线DE距离的是( )
 如图,AD⊥BC,ED⊥AB,表示点A到直线DE距离的是( )
如图,AD⊥BC,ED⊥AB,表示点A到直线DE距离的是( )| A. | 线段AD的长度 | B. | 线段AE的长度 | C. | 线段BE的长度 | D. | 线段DE的长度 |
15.在-1,0,-2,1这四个数中,最大的数是( )
| A. | -4 | B. | -2 | C. | 0 | D. | 1 |
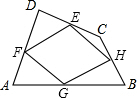 如图,顺次连接四边形ABCD各边中点得四边形EFGH,要使四边形EFGH为矩形,应添加的条件是AC⊥BD.
如图,顺次连接四边形ABCD各边中点得四边形EFGH,要使四边形EFGH为矩形,应添加的条件是AC⊥BD.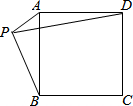 如图,P是正方形ABCD外一点,PA=$\sqrt{2}$,PB=4,则PD长度的最大值为6.
如图,P是正方形ABCD外一点,PA=$\sqrt{2}$,PB=4,则PD长度的最大值为6.