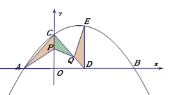题目内容
【题目】已知正方形ABCD的对角线相交于O,点P在射线AO上,∠MPN=90°.
(1)如图1,当P与点O重合,M、N分别在AD、AB上,AM=2DM,则![]() =__________;
=__________;
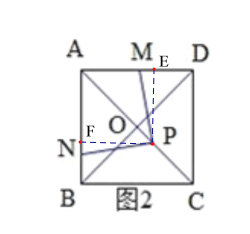
(2)如图2,点P在CO上,AP=2CP,M为AD的中点,求![]() 的值.
的值.
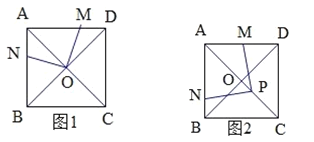
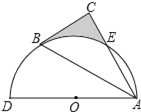
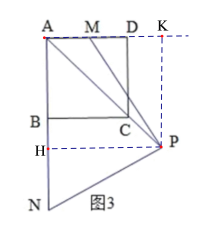
(3)如图3,P在AC的延长线上,M为AD的中点,AP=nCP,则![]() =____________(用含n的式子表示)
=____________(用含n的式子表示)

【答案】(1)![]() ;(2)
;(2)![]() =5;(3)
=5;(3)![]()
【解析】
(1)根据正方形的性质定理和三角形全等的判定定理,可得MODNOA,MOANOB,结合AM=2DM,即可得到结论;
(2)过点P作PF∥AD,PE∥AB,易得AE=2ED,设ED=a,则AE=2a,A =3a,MD=![]() ,ME =
,ME =![]() a,再证MEPNFP,可得AN=
a,再证MEPNFP,可得AN=![]() ,BN=
,BN=![]() a,进而即可得到结论;
a,进而即可得到结论;
(3)过点P作PK⊥AD交AD的延长线于点K,过点P作PH⊥AN于点H,易得![]() ,设DK=a,则AK=na,AD=(n-1)a,MK=
,设DK=a,则AK=na,AD=(n-1)a,MK=![]() ,由(2)题的方法得:MKPNHP,从而得AN=
,由(2)题的方法得:MKPNHP,从而得AN=![]() ,BN=
,BN=![]() ,进而即可得到结论.
,进而即可得到结论.
(1)∵正方形ABCD的对角线相交于O,
∴OA=OD,∠ODM=∠OAN=45°,∠AOD=90°,
∵∠MPN=90°,
∴∠MOD+∠AOM=∠NOA+∠AOM=90°,
∴∠MOD=∠NOA,
∴MODNOA(ASA),
∴DM=NA,
同理:MOANOB(ASA),
∴AM=BN,
∵AM=2DM,
∴BN=2 NA
∴![]() =
=![]() ,
,
故答案是:![]() ;
;
(2)过点P作PF∥AD,PE∥AB,
∴![]() ,
,
∵AP=2CP,
∴AE=2ED,
设ED=a,则AE=2a,AD=2a+a=3a,
∵M为AD的中点,
∴MD=![]() AD=
AD=![]() ×3a=
×3a=![]() ,ME=
,ME=![]() - a=
- a=![]() a,
a,
∵FG∥AD,PE∥AB,
∴PF⊥AB,PE⊥AD,
∵AC是∠BAD的平分线,
∴PF=PE,
∵∠BAD=90°,
∴四边形AEPF是正方形,即:∠EPF=90°,
∵∠MPN=90°,
∴∠EPM+∠MPF=∠FPN+∠MPF=90°,
∴∠EPM=∠FPN,
又∵∠MEP=∠NFP=90°,
∴MEPNFP(ASA),
∴ME=NF=![]() a,
a,
又∵AF=AE=2a,
∴AN=2a+![]() a=
a=![]() ,
,
∵AB=AD=3a,
∴BN=3a-![]() =
=![]() a,
a,
∴![]() =5;
=5;
(3)过点P作PK⊥AD交AD的延长线于点K,过点P作PH⊥AN于点H,
∵PK∥CD,AP=nCP,
∴![]() ,
,
设DK=a,则AK=na,AD=(n-1)a,
∵M为AD的中点,
∴MD=![]() ,
,
∴MK=MD+DK=![]() ,
,
由(2)题的方法得:MKPNHP(AAS),四边形AKPH是正方形,
∴HN=MK=![]() ,AH=AK=na,
,AH=AK=na,
∴AN=![]() +na=
+na=![]() ,BN=
,BN=![]() -(n-1)a=
-(n-1)a=![]() ,
,
∴![]() =
=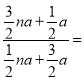
![]() .
.
故答案是:![]() .
.

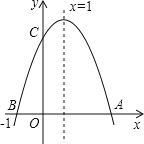
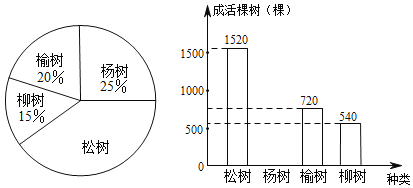
【题目】已知二次函数y=ax2+bx+c(a≠0)中的x和y满足下表:
x | … | 0 | 1 | 2 | 3 | 4 | 5 | … |
y | … | 3 | 0 | -1 | 0 | m | 8 | … |
(1)可求得m的值为________;
(2)在坐标系画出该函数的图象;
(3)当y≥0时,x的取值范围为_____________