题目内容
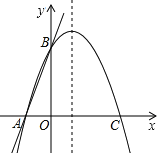
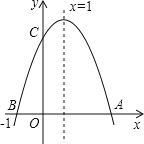
【题目】如图，二次函数y＝ax2+bx+c（b≠0）的图象与x轴交于A、B两点，与y轴交于点C，点B坐标（﹣1，0），下面的四个结论：①OA＝3 ②a+b+c＜0 ③ac＞0 ④当y＞0时，﹣1＜x＜3，其中正确的结论是（ ）
A.②④B.①③C.①④D.①②④
【答案】C
【解析】
根据二次函数的图象与性质逐一判断，①需要根据其对称性解答，②可以令
，在图象上看其对应的函数值，③需要根据图象得到
的正负，再判断，④观察函数值大于零时对应的自变量取值范围即可.
解：∵点B坐标（﹣1，0），对称轴是直线x＝1，
∴A的坐标是（3，0），
∴OA＝3，∴①正确；
∵由图象可知：当x＝1时，y＞0，
∴把x＝1代入二次函数的解析式得：y＝a+b+c＞0，∴②错误；
∵抛物线的开口向下，与y轴的交点在y轴的正半轴上，
∴a＜0，c＞0，
∴ac＜0，∴③错误；
∵由图象可知：当y＞0时，﹣1＜x＜3，∴④正确；
故选：C．
练习册系列答案
相关题目
