题目内容
5. 如图,已知△ABC,以AB为直径的⊙O交AC于点F,交BC于点D,且BD=CD,DF⊥AC于点F.给出以下四个结论:
如图,已知△ABC,以AB为直径的⊙O交AC于点F,交BC于点D,且BD=CD,DF⊥AC于点F.给出以下四个结论:①DF是⊙O的切线;②CF=EF;③$\widehat{AE}$=$\widehat{DE}$;④∠A=2∠FDC.
其中正确结论的序号是①②④.
分析 由BD=DC,OA=OB,推出OD是△ABC的中位线,OD∥AC,由DF⊥AC得出得DF⊥OD,即DF是⊙O的切线,然后证出△ABC是等腰三角形,得出∠B=∠C,再推出△CDE为等腰三角形,从而推出∠A=2∠FDC,CF=EF.最后由假设推出$\widehat{AE}$≠$\widehat{DE}$;③不正确;即可得出结果.
解答 解:连接OD、DE、AD,如图所示:
∵AB是⊙O的直径,
∴OA=OB,
∵DB=DC,
∴OD是△ABC的中位线,
∴OD∥AC,
∵DF⊥AC,
∴DF⊥OD.
∴DF是⊙O的切线,①正确;
∵DF是⊙O的切线,
∴∠CED=∠B,
∵AB是⊙O的直径,
∴∠ADB=90°,
即AD⊥BC,
∵BD=CD,
∴AB=AC,
∴∠B=∠C,
∴∠CED=∠C,
∴DC=DE,
又∵DF⊥AC,
∴CF=EF,②正确;
当∠EAD=∠EDA时,$\widehat{AE}=\widehat{DE}$,
此时△ABC为等边三角形,
当△ABC不是等边三角形时,
∠EAD≠∠EDA,
则$\widehat{AE}$≠$\widehat{DE}$,
∴$\widehat{AE}$=$\widehat{DE}$不正确;
∵DF⊥AC,AD⊥BC,
∴∠FDC+∠C=∠CAD+∠C=90°,
∴∠FDC=∠CAD,
又AB=AC,
∴∠BAD=∠CAD,
∴∠A=2∠CAD=2∠FDC,④正确;
故答案为:①②④.
点评 此题考查的知识点是切线的判定与性质、等腰三角形的判定与性质、圆周角定理、线段垂直平分线的性质、圆内接四边形的性质等知识;本题综合性强,熟练掌握等腰三角形的判定与性质及圆周角定理是解决问题的关键.

练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案
相关题目
17.化简2$\sqrt{4+2\sqrt{3}}$-$\sqrt{21-12\sqrt{3}}$的结果为( )
| A. | 5-4$\sqrt{3}$ | B. | 4$\sqrt{3}$-1 | C. | 5 | D. | 1 |
17. 如图中,如图的几何体展开图是( )
如图中,如图的几何体展开图是( )
 如图中,如图的几何体展开图是( )
如图中,如图的几何体展开图是( )| A. |  | B. |  | C. |  | D. |  |
 如图,直线y=kx+b经过A(1,-1)、B(-1,3),则-1<kx+b<3的解集为-1<x<1.
如图,直线y=kx+b经过A(1,-1)、B(-1,3),则-1<kx+b<3的解集为-1<x<1.
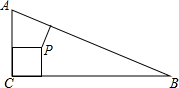 如图,在△ABC中,∠C=90°,两直角边AC=5,BC=12,在三角形内有一点P,它到各边的距离相等,则这个距离2.
如图,在△ABC中,∠C=90°,两直角边AC=5,BC=12,在三角形内有一点P,它到各边的距离相等,则这个距离2.