题目内容
16.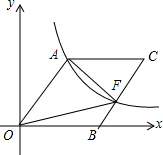 如图,O为坐标原点,四边形OACB是菱形,OB在x轴的正半轴上,sin∠AOB=$\frac{4}{5}$,反比例函数y=$\frac{48}{x}$在第一象限内的图象经过点A,与BC交于点F,则△AOF的面积等于( )
如图,O为坐标原点,四边形OACB是菱形,OB在x轴的正半轴上,sin∠AOB=$\frac{4}{5}$,反比例函数y=$\frac{48}{x}$在第一象限内的图象经过点A,与BC交于点F,则△AOF的面积等于( )| A. | 60 | B. | 80 | C. | 30 | D. | 40 |
分析 过点A作AM⊥x轴于点M,设OA=a,通过解直角三角形找出点A的坐标,结合反比例函数图象上点的坐标特征即可求出a的值,再根据四边形OACB是菱形、点F在边BC上,即可得出S△AOF=$\frac{1}{2}$S菱形OBCA,结合菱形的面积公式即可得出结论.
解答 解:过点A作AM⊥x轴于点M,如图所示.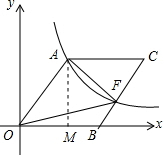
设OA=a,
在Rt△OAM中,∠AMO=90°,OA=a,sin∠AOB=$\frac{4}{5}$,
∴AM=OA•sin∠AOB=$\frac{4}{5}$a,OM=$\sqrt{O{A}^{2}-A{M}^{2}}$=$\frac{3}{5}$a,
∴点A的坐标为($\frac{3}{5}$a,$\frac{4}{5}$a).
∵点A在反比例函数y=$\frac{48}{x}$的图象上,
∴$\frac{3}{5}$a×$\frac{4}{5}$a=$\frac{12}{25}{a}^{2}$=48,
解得:a=10,或a=-10(舍去).
∴AM=8,OM=6,OB=OA=10.
∵四边形OACB是菱形,点F在边BC上,
∴S△AOF=$\frac{1}{2}$S菱形OBCA=$\frac{1}{2}$OB•AM=40.
故选D.
点评 本题考查了菱形的性质、解直角三角形以及反比例函数图象上点的坐标特征,解题的关键是找出S△AOF=$\frac{1}{2}$S菱形OBCA.

 53随堂测系列答案
53随堂测系列答案| A. | a+2a=3a | B. | (a2)3=a6 | C. | a2•a3=a5 | D. | a6÷a3=a2 |
| A. | 8是a的因子,8是b的因子 | B. | 8是a的因子,8不是b的因子 | ||
| C. | 8不是a的因子,8是c的因子 | D. | 8不是a的因子,8不是c的因子 |
所谓气质,是指婴儿出生后最早表示出来的以一种较为明显而稳定的人格特征类型,也指孩子对身体内在或外来刺激反应的方式。心理学界常将气质分为四大类:胆汁型、多血质、黏液质、抑郁质。我校心理协会为了更好的了解学生,在高中随机发放了若干份问卷调查,并将统计结果绘制成如下图表:
四种气质类型人数频数分布表 | 黏液质气质各年级人数频数分布直方图 | |||||||||||||||
|
|
根据以上信息完成下列问题并补全频数分布直方图:
(1)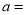 _______,
_______, 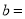 _______
_______
(2)请你估计一下,高三年级1200名学生中,胆汁型和多血质的共有多少人?
 如图,CD是⊙O的直径,若AB⊥CD,垂足为B,∠OAB=40°,则∠C等于25度.
如图,CD是⊙O的直径,若AB⊥CD,垂足为B,∠OAB=40°,则∠C等于25度. 如图,几何体是由3个大小完全一样的正方体组成的,它的左视图是( )
如图,几何体是由3个大小完全一样的正方体组成的,它的左视图是( )



 如图是几何体的俯视图,所表示数字为该位置小正方体的个数,则该几何体的正视图是( )
如图是几何体的俯视图,所表示数字为该位置小正方体的个数,则该几何体的正视图是( )



 某国发生8.1级强烈地震,我国积极组织抢险队赴地震灾区参与抢险工作,如图,某探测队在地面A、B两处均探测出建筑物下方C处有生命迹象,已知探测线与地面的夹角分别是25°和60°,且AB=4米,求该生命迹象所在位置C的深度.(结果精确到1米,参考数据:sin25°≈0.4,cos25°≈0.9,tan25°≈0.5,$\sqrt{3}$≈1.7)
某国发生8.1级强烈地震,我国积极组织抢险队赴地震灾区参与抢险工作,如图,某探测队在地面A、B两处均探测出建筑物下方C处有生命迹象,已知探测线与地面的夹角分别是25°和60°,且AB=4米,求该生命迹象所在位置C的深度.(结果精确到1米,参考数据:sin25°≈0.4,cos25°≈0.9,tan25°≈0.5,$\sqrt{3}$≈1.7)