题目内容
5.计算:(1)(a+b)2-b(2a+b)(2)($\frac{2-2x}{x+1}$+x-1)÷$\frac{{x}^{2}-x}{x+1}$.
分析 (1)根据完全平方公式和单项式乘多项式的法则计算即可;
(2)根据分式的混合运算法则进行计算.
解答 解:(1)(a+b)2-b(2a+b)
=a2+2ab+b2-2ab-b2
=a2;
(2)($\frac{2-2x}{x+1}$+x-1)÷$\frac{{x}^{2}-x}{x+1}$
=$\frac{2-2x+{x}^{2}-1}{x+1}$×$\frac{x+1}{{x}^{2}-x}$
=$\frac{({x-1)}^{2}}{x+1}$×$\frac{x+1}{x(x-1)}$
=$\frac{x-1}{x}$.
点评 本题考查的是整式的混合运算、分式的混合运算,掌握完全平方公式、分式的混合运算法则是解题的关键.

练习册系列答案
相关题目
15.计算 (2x+1)(x-1)-(x2+x-2)的结果,与下列哪一个式子相同?( )
| A. | x2-2x+1 | B. | x2-2x-3 | C. | x2+x-3 | D. | x2-3 |
16.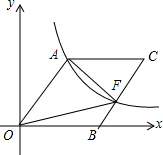 如图,O为坐标原点,四边形OACB是菱形,OB在x轴的正半轴上,sin∠AOB=$\frac{4}{5}$,反比例函数y=$\frac{48}{x}$在第一象限内的图象经过点A,与BC交于点F,则△AOF的面积等于( )
如图,O为坐标原点,四边形OACB是菱形,OB在x轴的正半轴上,sin∠AOB=$\frac{4}{5}$,反比例函数y=$\frac{48}{x}$在第一象限内的图象经过点A,与BC交于点F,则△AOF的面积等于( )
 如图,O为坐标原点,四边形OACB是菱形,OB在x轴的正半轴上,sin∠AOB=$\frac{4}{5}$,反比例函数y=$\frac{48}{x}$在第一象限内的图象经过点A,与BC交于点F,则△AOF的面积等于( )
如图,O为坐标原点,四边形OACB是菱形,OB在x轴的正半轴上,sin∠AOB=$\frac{4}{5}$,反比例函数y=$\frac{48}{x}$在第一象限内的图象经过点A,与BC交于点F,则△AOF的面积等于( )| A. | 60 | B. | 80 | C. | 30 | D. | 40 |
13.下列调查中,最适合采用全面调查(普查)方式的是( )
| A. | 对重庆市辖区内长江流域水质情况的调查 | |
| B. | 对乘坐飞机的旅客是否携带违禁物品的调查 | |
| C. | 对一个社区每天丢弃塑料袋数量的调查 | |
| D. | 对重庆电视台“天天630”栏目收视率的调查 |
10.下列说法中不正确的是( )
| A. | 函数y=2x的图象经过原点 | |
| B. | 函数y=$\frac{1}{x}$的图象位于第一、三象限 | |
| C. | 函数y=3x-1的图象不经过第二象限 | |
| D. | 函数y=-$\frac{3}{x}$的值随x的值的增大而增大 |

 +|b-8|+(c-10)2=0,则△ABC是( )
+|b-8|+(c-10)2=0,则△ABC是( ) +5.,若x★2=6,则实数x的值是 _________。
+5.,若x★2=6,则实数x的值是 _________。