先化简.再求值:(2a2b-5ab+1)-(3ab+2a2b).其中a=-3.b=$\frac{1}{3}$．题目和参考答案——青夏教育精英家教网—

题目内容

18．先化简，再求值：（2a²b-5ab+1）-（3ab+2a²b），其中a=-3，b=$\frac{1}{3}$．

分析原式去括号合并得到最简结果，把a与b的值代入计算即可求出值．

解答解：原式=2a²b-5ab+1-3ab-2a²b=-8ab+1，
当a=-3，b=$\frac{1}{3}$时，原式=8+1=9．

点评此题考查了整式的加减-化简求值，熟练掌握去括号法则与合并同类项法则是解本题的关键．

练习册系列答案

相关题目

9．在数轴上，与2所在的点距离是2个单位长度的点所表示的数是（　　）

6．如果3x^2n-1y^m与-5x^my³是同类项，则m和n的值分别为（　　）

13．

油桶制造厂的某车间主要负责生产制造油桶用的圆形铁片和长方形铁片，该车间有工人42人，每个工人平均每小时可以生产圆形铁片102片或者长方形铁片80片，如图，一个油桶由两个圆形铁片和一个长方形铁片相配套，生产圆形铁片和长方形铁片的工人各为多少人时，才能使生产的铁片恰好配套？

3．

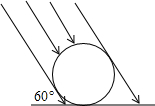如图，太阳光线与地面成60°的角，照在地面的一只排球上，排球在地面的投影长是14$\sqrt{3}$cm，则排球的直径是（　　）

10．

我市某工艺厂设计了一款成本为10元/件的工艺品投放市场进行试销，经过市场调查，得到如下数据：

销售单价x（元/件）	…	20	30	40	50	60	…
每天销售量y（件）	…	500	400	300	200	100	…

（1）把上表中x、y的各组对应值作为点的坐标，在给出的平面直角坐标系中描出相应的点，猜想y与x的函数关系，并求出函数关系式及自变量x的取值范围；
（2）若市物价部门规定，该工艺品销售单价最高不能超过35元/件，那么销售单价定为多少时，工艺厂试销该工艺品每天获得的利润最大？最大利润是多少？

7．将点A（2$\sqrt{2}$，0）绕着原点按逆时针方向旋转135°得到点B，则点B的坐标为（-2，2）．

9．

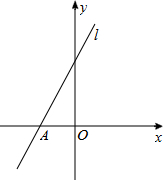如右图，在直角坐标系中，点A（-4，0），直线l与x轴夹角为60°，点B在直线l上，且AB=10，求点B的坐标．

试题分类