题目内容
3．
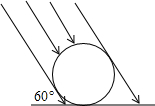如图，太阳光线与地面成60°的角，照在地面的一只排球上，排球在地面的投影长是14$\sqrt{3}$cm，则排球的直径是（ ）| A． | 7cm | B． | 14cm | C． | 21cm | D． | 21$\sqrt{3}$cm |
分析 由于太阳光线为平行光线，根据切线的性质得到AB为排球的直径，CD=AB，CE=14$\sqrt{3}$cm，在Rt△CDE中，利用正弦的定义可计算出CD的长，从而得到排球的直径．
解答 解：如图，点A与点B为太阳光线与球的切点，
则AB为排球的直径，CD=AB，CE=14$\sqrt{3}$cm，
在Rt△CDE中，sinE=$\frac{CD}{CE}$，
所以CD=14$\sqrt{3}$•sin60°=14$\sqrt{3}$×$\frac{\sqrt{3}}{2}$=21，
即排球的直径为21cm．
故选：C．
点评 本题考查了解直角三角形和平行投影：由平行光线形成的投影是平行投影，如物体在太阳光的照射下形成的影子就是平行投影；平行投影中物体与投影面平行时的投影是全等的．
练习册系列答案
相关题目
13．
实施新课程改革以来，某校开设了综合实践课，为了了解同学们对该课程的看法，对400名同学作了问卷调查，并将调查结果绘制成如图的扇形统计图．
（1）分别计算出持每一种意见的确定人数，填写在下表中．
（2）从扇形统计图与统计数据中你能得出什么结论？说说你的理由．
实施新课程改革以来，某校开设了综合实践课，为了了解同学们对该课程的看法，对400名同学作了问卷调查，并将调查结果绘制成如图的扇形统计图．（1）分别计算出持每一种意见的确定人数，填写在下表中．
| 意见 | 非常喜欢 | 喜欢 | 有一点喜欢 | 不喜欢 |
| 人数 |
如图，在△ABC中，AB=AC=2，∠B=40°，点D在线段AB上运动（D不与B、C重合），连接AD，作∠ADE=40°，DE交线AC段于E．
11．一个粮库至8月31日有存粮112吨，从9月1日至9月10日，该粮库粮食进出情况如下表（记进库为正）．
（1）至9月10日运粮结束时，仓库内存粮为多少吨？
（2）9月1日至9月10日共进出粮食多少吨？
| 日 期 | 1日 | 2日 | 3日 | 4日 | 5日 | 6日 | 7日 | 8日 | 9日 | 10日 |
| 数量（吨） | 50 | -11 | -21 | 41 | 89 | -72 | 86 | 0 | -54 | -12 |
（2）9月1日至9月10日共进出粮食多少吨？
12．（m+n）-2（m-n）的计算结果是（ ）
| A． | 3n-2m | B． | 3n+m | C． | 3n-m | D． | 3n+2m |