题目内容
 如图,点B在⊙O的直径AC的延长线上,点D在⊙O上,AD=DB,∠B=30°,若⊙O的半径为4.
如图,点B在⊙O的直径AC的延长线上,点D在⊙O上,AD=DB,∠B=30°,若⊙O的半径为4.(1)求证:BD是⊙O的切线;
(2)求CB的长.
考点:切线的判定
专题:
分析:(1)连接OD,由条件可求得∠COD=60°,进一步可求得∠ODB=90°,可得出结论;
(2)在Rt△OBD中,利用勾股定理可求得OB的长,结合半径可求得CB的长.
(2)在Rt△OBD中,利用勾股定理可求得OB的长,结合半径可求得CB的长.
解答: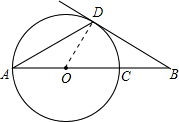 (1)证明:
(1)证明:
连接OD,
∵AD=DB,∠B=30°,
∴∠A=∠B=30°,
∴∠COD=60°,
∴∠ODC=180°-30°-60°=90°,
∴OD⊥BD,
∵OD是☉O的半径,
∴BD是☉O的切线;
(2)解:
在Rt△OBD中,
∵∠ODB=90°,∠B=30°,
∴OB=2OD=8,
∵OB=4,
∴CB=4.
 (1)证明:
(1)证明:连接OD,
∵AD=DB,∠B=30°,
∴∠A=∠B=30°,
∴∠COD=60°,
∴∠ODC=180°-30°-60°=90°,
∴OD⊥BD,
∵OD是☉O的半径,
∴BD是☉O的切线;
(2)解:
在Rt△OBD中,
∵∠ODB=90°,∠B=30°,
∴OB=2OD=8,
∵OB=4,
∴CB=4.
点评:本题主要考查切线的判定及直角三角形的性质,掌握切线的两种判定方法是解题的关键,并注意直角三角形性质的利用.

练习册系列答案
相关题目
下列名人中,①鲁迅、②姚明、③刘徽、④杨利伟、⑤高斯、⑥贝多芬、⑦陈景润、⑧祖冲之.其中是数学家的为( )
| A、①③⑤⑧ | B、③⑤⑦⑧ |
| C、②④⑥⑧ | D、④⑤⑥⑧ |
 如图,以点P为圆心,以2
如图,以点P为圆心,以2 已知:如图,AD、BC相交于点O,OA=OB,∠C=∠D.
已知:如图,AD、BC相交于点O,OA=OB,∠C=∠D.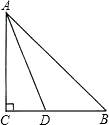 Rt△ABC中,∠C=90°,∠B=45°,AD平分∠BAC,
Rt△ABC中,∠C=90°,∠B=45°,AD平分∠BAC, 如图,在Rt△ABC中,∠C=90°,按要求填空:
如图,在Rt△ABC中,∠C=90°,按要求填空: 抛物线y=x2-4x+3
抛物线y=x2-4x+3 如图,交警统计了某个时段在一个路口来往车辆的车速(单位:千米/时)情况,则该时段内来往车辆的平均速度是
如图,交警统计了某个时段在一个路口来往车辆的车速(单位:千米/时)情况,则该时段内来往车辆的平均速度是