题目内容
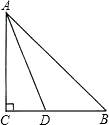 Rt△ABC中,∠C=90°,∠B=45°,AD平分∠BAC,
Rt△ABC中,∠C=90°,∠B=45°,AD平分∠BAC,(1)过点D作DE⊥AB,垂足为E(尺规作图,保留作图痕迹,不写作法);
(2)线段AC,CD,AB之间的数量关系是什么?请说明理由.
考点:角平分线的性质,等腰直角三角形
专题:
分析:(1)以点D为圆心,适当长为半径画弧,交BA于两点,以这两点为圆心,大于这两点距离的一半为半径画弧,交BA的上方于一点,作过这点和点D的直线交BA于点E;
(2)根据AAS可以证明△ACD≌△AED,得AE=AC,DE=CD.根据等腰直角三角形的性质,得∠B=45°,则∠BED=45°,从而证明DE=BE,则可得出AB=AC+CD.
(2)根据AAS可以证明△ACD≌△AED,得AE=AC,DE=CD.根据等腰直角三角形的性质,得∠B=45°,则∠BED=45°,从而证明DE=BE,则可得出AB=AC+CD.
解答:解:(1)如图,

(2)AB=AC+CD,理由如下:
∵AD是∠BAC的平分线,
∴∠CAD=∠EAD.
在△ACD与△AED中,
,
∴△ACD≌△AED(AAS),
∴AC=AE,CD=ED.
∵∠BED=90°,∠B=45°,
∴∠BDE=∠B=45°,
∴DE=BE,
∴AB=AE+BE=AC+CD.

(2)AB=AC+CD,理由如下:
∵AD是∠BAC的平分线,
∴∠CAD=∠EAD.
在△ACD与△AED中,
|
∴△ACD≌△AED(AAS),
∴AC=AE,CD=ED.
∵∠BED=90°,∠B=45°,
∴∠BDE=∠B=45°,
∴DE=BE,
∴AB=AE+BE=AC+CD.
点评:此题考查了角平分线的性质,全等三角形的判定与性质,等腰直角三角形的性质,以及过一点作已知直线的垂线,难度适中.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
若
=7,则10y-2的值( )
| 5y-1 |
| 2 |
| A、14 | B、28 | C、30 | D、32 |
 如图,以AD为直径的半圆O经过Rt△ABC斜边AB的两个端点,交直角边AC于点E,B、E是半圆弧的三等分点,
如图,以AD为直径的半圆O经过Rt△ABC斜边AB的两个端点,交直角边AC于点E,B、E是半圆弧的三等分点,
 如图,点B在⊙O的直径AC的延长线上,点D在⊙O上,AD=DB,∠B=30°,若⊙O的半径为4.
如图,点B在⊙O的直径AC的延长线上,点D在⊙O上,AD=DB,∠B=30°,若⊙O的半径为4.